
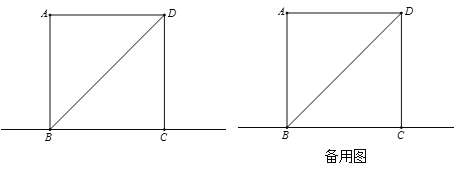
����Ŀ����ͼ����֪���κ���y��ax2+bx+c��ͼ����x���ཻ��A����1��0����B��3��0�����㣬��y���ཻ�ڵ�C��0��3��
��1����������κ����ı���ʽ��ֱ��д���������ꣻ
��2����P�ǵ�һ������������κ�����ͼ��������һ�㣬PH��x���ڵ�H����BC���ڵ�M������PC�����P�ĺ�����Ϊt
�����߶�PM�����ֵ��
��S��PBM��S��MHB��1��2ʱ����tֵ��
������PCM�ǵ���������ʱ��ֱ��д��P�����꣮
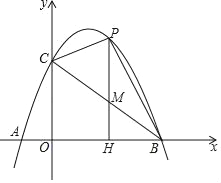
���𰸡���1����1��4����2����![]() ��
��![]() ������PCM�ǵ���������ʱ����P������Ϊ��2��3����3��
������PCM�ǵ���������ʱ����P������Ϊ��2��3����3��![]() ����2+4
����2+4![]() ����1��4����
����1��4����
��������
�躯������ʽΪy��ax2+bx+c����A����1��0����B��3��0����C��0��3�����뼴����
������ֱ��BC�ı���ʽ�������P�ĺ�����Ϊt��Ȼ��PM�ij���ʾ�ɺ�������ʽ������;
����S��PBM��S��MHB��1��2ת���ɵ�֮��MH��2PM��������P��M�����꣬�г���ʽ���������ֵ���پ����ɵã�
�����������PC=PM��PC=CM��PM=CM���t��ֵ���ټ��飬���ɵ�.
��1����A����1��0����B��3��0����C��0��3������y��ax2+bx+c���ã�
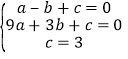 �����
����� ��
��
����κ����ı���ʽΪy����x2+2x+3��
��y����x2+2x+3������x��1��2+4��
����κ���ͼ��Ķ�������Ϊ��1��4����
��2������ֱ��BC�ı���ʽΪy��mx+n��m��0����
��B��3��0����C��0��3������y��mx+n���ã�
![]() ����ã�
����ã�![]() ��
��
��ֱ��BC�ı���ʽΪy����x+3��
�ߵ�P�ĺ�����Ϊt��0��t��3����
���P��������t����t2+2t+3������M��������t����t+3����
��PM����t2+2t+3������t+3������t2+3t������t��![]() ��2+
��2+![]() ��
��
���߶�PM�����ֵΪ![]() ��
��
�ڡߵ�P������Ϊ��t����t2+2t+3������M������Ϊ��t����t+3����
���H��������t��0����
��PM����t2+2t+3������t+3������t2+3t��MH����t+3��
�ߡ�PBM����MHB�ȸߣ�S��PBM��S��MHB��1��2��
��MH��2PM������t+3����2t2+6t��
��ã�t1��![]() ��t2��3���������⣬��ȥ����
��t2��3���������⣬��ȥ����
�൱S��PBM��S��MHB��1��2ʱ��t��ֵΪ![]() ��
��
�ۡߵ�P������Ϊ��t����t2+2t+3������M������Ϊ��t����t+3������C������Ϊ��0��3����
��PM����t2+2t+3������t+3������t2+3t��CM��![]() ��PC��
��PC��![]() ��
��
��PM��PCʱ���Щ�t2+3t��![]() ��
��
��0��t��3��
��ԭ���̿�����Ϊ��2t��4��0��
��ã�t��2��
���P��������2��3����
��PM��CMʱ���Щ�t2+3t��![]() t��
t��
��ã�t1��0����ȥ����t2��3��![]() ��
��
���P��������3��![]() ����2+4
����2+4![]() ����
����
��CM��PCʱ����![]() t��
t��![]() ��
��
��0��t��3��
��ԭ���̿�����Ϊ��t2��4t+3��0��
��ã�t1��1��t2��3����ȥ����
���P��������1��4����
��������������PCM�ǵ���������ʱ����P������Ϊ��2��3����3��![]() ����2+4
����2+4![]() ����1��4����
����1��4����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AD�ǡ�ABC�Ľ�ƽ���ߣ�DE��DF�ֱ��ǡ�ABD�͡�ACD�ĸߣ��õ������ĸ����ۣ�

��AD��EF���ഹֱƽ�֣�
��AE=AF��
�۵���BAC=90��ʱ��AD=EF��
��DE��AB�Ĵ�ֱƽ���ߣ�
������ȷ����_________________(�����)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ijˮƽ�����Ͻ�����ĸ߶�ΪAB���ڵ�D�͵�F���ֱ���������2�ı��CD��EF����������52�������ҽ�����AB�����CD��EF��ͬһ��ֱƽ�������ӱ��CD����2����G������G����ý����ﶥ��A�ͱ�˶���C��ͬһ��ֱ�������ӱ��FE����4����H������H����ý����ﶥ��A�ͱ�˶���E��ͬһ��ֱ������������ĸ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�ڡ����˶����ҿ��֡��ļ��ܱ�����ѵ��У�����ͬ�����£��Լס�������ͬѧ�ġ�����������Ŀ������5�β��ԣ����Գɼ�����λ���֣����£�������ͼ�ж���ȷ���ǣ� ��

A.�׳ɼ���ƽ���ֵ����ҳɼ���ƽ���֣�
B.�׳ɼ�����λ�������ҳɼ�����λ����
C.�׳ɼ������������ҳɼ���������
D.�׳ɼ��ķ�������ҳɼ��ķ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�ֱ��l1��![]() ����A��3��0��������ֱ��l2��
����A��3��0��������ֱ��l2��![]() ���ڵ�B��m��1����
���ڵ�B��m��1����
��1����ֱ��l1��![]() �ĺ�������ʽ��
�ĺ�������ʽ��
��2��������P��n��0���Ҵ���x���ֱ����l1��l2�ֱ��ڵ�C��D������Cλ�ڵ�D�Ϸ�ʱ��ֱ��д��n��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У���E��BC������ֱ����һ���㣨�����B��C�غϣ�������B��BF��DE��������DE�ڵ�F������CF��
��1����ͼ������E���߶�BC��ʱ����BDF=����
�ٰ�Ҫ��ȫͼ�Σ�
�ڡ�EBF=______________���ú�����ʽ�ӱ�ʾ����
���ж��߶� BF��CF��DF֮���������ϵ����֤����
��2������E��ֱ��BC��ʱ��ֱ��д���߶�BF��CF��DF֮���������ϵ������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+3x+c����A����1��0����B��4��0�����㣬��y�ύ�ڵ�C��
��1���������ߵĽ���ʽ��
��2������P�ڵ�һ�����������ϣ��ҵ�P�ĺ�����Ϊt������P��x�������߽�ֱ��BC�ڵ�Q�����߶�PQ�ij�Ϊm����m��t֮��ĺ�����ϵʽ�������m�����ֵ��
��3����x�����Ƿ���ڵ�E��ʹ�Ե�B��C��EΪ�����������Ϊ���������Σ�������ڣ�ֱ��д��E�����ꣻ��������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڶ���ȫ�������˶��Ὣ��2019��8����̫ԭ��Ļ������ɽ����ʷ�ϵ�һ�ξٰ�ȫ�������ۺ����˶��ᣬ�ؽ��ƶ�����ȫ����������.ij������Ʒ�̵���ڹ����ס��������˶�����50������������2000Ԫ����������2400Ԫ.�̵꽫�����˶��������۵��۶�Ϊ60Ԫ�������˶��������۵��۶�Ϊ88Ԫ.�õ�����һ��ʱ����֣������˶��������۲����룬���ǽ����µ��˶��������������ۣ��������˶��������ۼ۸�.�̵������������˶������ٿɻ���2460Ԫ��������˶�����ԭ�����ۼ�������Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)���ⷢ��
��ͼ1����ACB�͡�DCE��Ϊ�ȱ������Σ���A��D��E��ͬһֱ���ϣ�����BE����գ�
����AEB�Ķ���Ϊ______��
���߶�AD��BE֮���������ϵΪ______��
(2)��չ̽��
��ͼ2����ACB�͡�DCE��Ϊ����ֱ�������Σ���ACB����DCE��90�㣬��A��D��E��ͬһֱ���ϣ�CMΪ��DCE��DE���ϵĸߣ�����BE�����жϡ�AEB�Ķ������߶�CM��AE��BE֮���������ϵ����˵�����ɣ�

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com