
����Ŀ����֪����ͼ����Rt��ACB�У���C=90����AC=4cm��BC=3cm����P��B������BA�������A�����˶����ٶ�Ϊ1cm/s����Q��A������AC�������C�����˶����ٶ�Ϊ2cm/s������PQ�������˶���ʱ��Ϊt��s����0��t��2��������������⣺
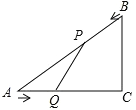
��1������AQP�����Ϊy��cm2������y��t֮��ĺ�����ϵʽ��
��2���Ƿ����ijһʱ��t��ʹ�߶�PQǡ�ð�Rt��ACB���ܳ������ͬʱƽ�֣������ڣ������ʱt��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��y=��![]() t2+3t����2����������һʱ��t��ʹ�߶�PQ��Rt��ACB���ܳ������ͬʱƽ�֣�
t2+3t����2����������һʱ��t��ʹ�߶�PQ��Rt��ACB���ܳ������ͬʱƽ�֣�
��������
�����������1����������APQ�������Ҫ��ȷ���ױߺߵ�ֵ���ױ�AQ���Ը���Q���ٶȺ�ʱ��t��ʾ�������ؼ��Ǹߣ�������AP����A������ֵ����AP�ij�������AB��BP��ã���sinA����BC��AB��ֵ����˱�ʾ��AQ��AQ���ϵĸߺͿ��Եó�y��t�ĺ�����ϵʽ��
��2�������������ABC���ܳ������ƽ�֣���ôAP+AQ=BP+BC+CQ����ô������t��ʾ��CQ��AQ��AP��BP�ij�����ô���������ʱt��ֵ�����ǿɽ�t��ֵ���루1���������t�Ĺ�ϵʽ�У������ʱ����Ƕ��٣�Ȼ������Ƿ���������ABC�����һ�룬�Ӷ��жϳ��Ƿ������һʱ�̣�
�⣺��1������P��PH��AC��H��
�ߡ�APH�ס�ABC��
��![]() =
=![]() ��
��
��![]() =
=![]() ��
��
��PH=3��![]() t��
t��
��y=![]() ��AQ��PH=
��AQ��PH=![]() ��2t����3��
��2t����3��![]() t��=��
t��=��![]() t2+3t��
t2+3t��
��2�������ڣ�
���ɣ�����PQ����ABC�ܳ�ƽ�֣�
��AP+AQ=BP+BC+CQ��
����5��t��+2t=t+3+��4��2t�������t=1��
��PQ����ABC���ƽ�֣���S��APQ=![]() S��ABC����
S��ABC����![]() t2+3t=3��
t2+3t=3��
��t=1�������淽�̲�������
����������һʱ��t��ʹ�߶�PQ��Rt��ACB���ܳ������ͬʱƽ�֣�




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У������A����B����C=2��3��5���Ƿ֣�����һ��__�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ʾ����A��B����֮��������վCվ���ͳ���A��ʻ��Cվ��������B��ʻ��A�أ�����ͬʱ������������ʻ��ͼ2�ǿͳ���������Cվ��·��y1��y2��ǧ�ף�����ʻʱ��x��Сʱ��֮��ĺ�����ϵͼ��
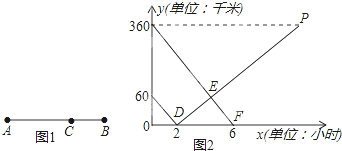
��1����գ�A��B������� ǧ�ף��������ٶ��� ǧ��/ʱ��
��2������Сʱ������Cվ��·��y2����ʻʱ��x֮��ĺ�������ʽ��
��3���͡���������ʱ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ������������Σ���������֧Ԯƶ��ɽ��ѧУ�����мס�����ľ���飬��ÿ����������16�ף���ÿ�������αȼ�8�ף�����������Щ���α��ҵ����������20�죬ѧУÿ�츶����80Ԫ�����ѣ�������120Ԫ�����ѡ�
(1)����ѧ�����������Σ�
(2)�����������У�ѧУҪ��һ�����˽��������ල��ѧУ������ÿ��10Ԫ������ѣ�����������������:a���ɼ���������b�����ҵ���������c���ס��Һ���ͬʱ����������Ϊ���ַ���ʡʱ��ʡǮ��Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABCDһ���Խ��߳�Ϊ6����AB��Ϊ����y2��7y+10=0��һ������������ABCD�ܳ�Ϊ�� ��
A�� 8 B�� 20 C�� 8��20 D�� 10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC��D��BC���ϵ�һ�㣬DE��AB��DF��AC������ֱ�ΪE��F������һ��������ʹDE=DF����˵�����ɣ�
�⣺������������ ��
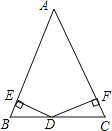
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ʒ���˶����������ν��ۣ�ÿ�����ۼ���560Ԫ��Ϊ315Ԫ����֪���ν��۵İٷ�����ͬ����ÿ�ν��۵İٷ��ʣ���ÿ�ν��۵İٷ���Ϊx���������еķ�������ȷ���ǣ� ��
A��560��1+x��2=315 B��560��1��x��2=315
C��560��1��2x��2=315 D��560��1��x2��=315
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һЩ������ɵ�ͼ����

��1���ڵڢٸ�ͼ���� ���������ڵڢڸ�ͼ���� ���������ڵڢ۸�ͼ���� ��������
��2���������ַ�ʽ����ȥ���ڵ�n��ͼ���ö��ٸ�������
��3������һ�°�121������ʱ���ǵڼ���ͼ����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com