
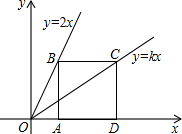
 如图,已知四边形ABCD是正方形,点B,C分别在两条直线y=2x和y=kx上,点A,D是x轴上两点.
如图,已知四边形ABCD是正方形,点B,C分别在两条直线y=2x和y=kx上,点A,D是x轴上两点.分析 根据正方形的边长,运用正方形的性质表示出C点的坐标,再将C的坐标代入函数中,从而可求得k的值.
解答  解:(1)∵正方形边长为2,
解:(1)∵正方形边长为2,
∴AB=2,
在直线y=2x中,当y=2时,x=1,
∴OA=1,OD=1+2=3,
∴C(3,2),
将C(3,2)代入y=kx,得2=3k,
∴k=$\frac{2}{3}$;
故答案为:$\frac{2}{3}$;
(2)k的值不会发生变化,
理由:∵正方形边长为a,
∴AB=a,
在直线y=2x中,当y=a时,x=$\frac{a}{2}$,
∴OA=$\frac{a}{2}$,OD=$\frac{3}{2}a$,
∴C($\frac{3}{2}a$,a),
将C($\frac{3}{2}a$,a)代入y=kx,得a=k×$\frac{3}{2}a$,
∴k=$\frac{2}{3}$.
点评 本题主要考查正方形的性质与正比例函数的综合运用,是一道比较好的题目,难度适中.灵活运用正方形的性质是解题的关键.


 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:解答题
 如图,在正方形ABCD中,F是DC的中点,E是BC上的一点,且EC=$\frac{1}{4}$BC=1,试判断AF与EF是否垂直,并说明理由.
如图,在正方形ABCD中,F是DC的中点,E是BC上的一点,且EC=$\frac{1}{4}$BC=1,试判断AF与EF是否垂直,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某地某天的温度变化情况如图所示,观察表格回答下列问题:
某地某天的温度变化情况如图所示,观察表格回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com