
科目:初中数学 来源: 题型:
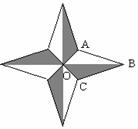
如图是“北大西洋公约组织”标志的主体部分(平面图),它是由四边形OABC绕点O进行3次旋转变换后形成的.测得AB=BC,OA=OC,∠ABC=40°,则∠OAB的度数是( )
A.115° B.116 ° C.117° D.137.5°
查看答案和解析>>
科目:初中数学 来源: 题型:
为改善城市生态环境,实现城市生活垃圾减量化、资源化、无害化的目标,杭州市决定从2010年3月1日起,在全市部分社区试点实施生活垃圾分类处理. 某街道计划建造垃圾初级处理点20个,解决垃圾投放问题. 有A、B两种类型处理点的占地面积、可供使用居民楼幢数及造价见下表:
| 类型 | 占地面积/m2 | 可供使用幢数 | 造价(万元) |
| A | 15 | 18 | 1.5 |
| B | 20 | 30 | 2.1 |
已知可供建造垃圾初级处理点占地面积不超过370m2,该街道共有490幢居民楼.
(1)满足条件的建造方案共有几种?写出解答过程.
(2)通过计算判断,哪种建造方案最省钱,最少需要多少万元.
查看答案和解析>>
科目:初中数学 来源: 题型:
边长为1的正方形OA B
B C
C 的顶点A
的顶点A 在X轴的正半轴上,如图将正方形OA
在X轴的正半轴上,如图将正方形OA B
B C
C 绕顶点O顺时针旋转75°得正方形OABC,使点B恰好落在函数y=ax2(a<0)的图像上,
绕顶点O顺时针旋转75°得正方形OABC,使点B恰好落在函数y=ax2(a<0)的图像上,
则a的值为___________.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
阅读以下的材料:
如果两个正数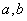 ,即
,即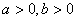 ,有下面的不等式:
,有下面的不等式:
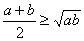 当且仅当
当且仅当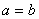 时取到等号
时取到等号
我们把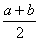 叫做正数
叫做正数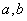 的算术平均数,把
的算术平均数,把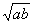 叫做正数
叫做正数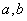 的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数。它在数学中有广泛的应用,是解决最值问题的有力工具。下面举一例子:
的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数。它在数学中有广泛的应用,是解决最值问题的有力工具。下面举一例子:
例:已知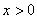 ,求函数
,求函数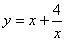 的最小值。
的最小值。
解:令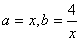 ,则有
,则有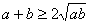 ,得
,得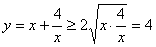 ,当且仅当
,当且仅当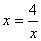 时,即
时,即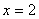 时,函数有最小值,最小值为
时,函数有最小值,最小值为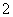 。
。
根据上面回答下列问题
① 已知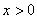 ,则当
,则当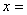 时,函数
时,函数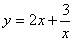 取到最小值,最小值
取到最小值,最小值
为 ;
② 用篱笆围一个面积为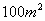 的矩形花园,问这个矩形的长、宽各为多
的矩形花园,问这个矩形的长、宽各为多 少时,所
少时,所
用的篱笆最短,最短的篱 笆周长是多少;
笆周长是多少;
③. 已知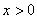 ,则自变量
,则自变量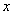 取何值时,函数
取何值时,函数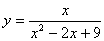 取到最大值,最大值为多少?
取到最大值,最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
若⊙O的半径为4 cm,点A到圆心O的距离为3 cm,那么点A与⊙O的位置关系是( )
A.点A在圆内 B.点A在圆上 C.点A在圆外 D.不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com