
分析 (1)先把二次根式化为最简二次根式,然后去绝对值后合并即可;
(2)先把方程化为整式方程,解整式方程得到x=1,然后进行检验确定原方程的解.
解答 (1)解:原式=$2\sqrt{3}+2-\sqrt{3}+3$
=$\sqrt{3}+5$;
(2)解:去分母得3(x+1)=6,解得x=1,
检验:把x=1代入x2-1=0,则x=1为原方程的增根,
所以原方程无解.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.也考查了解分式方程.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
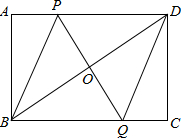 如图,在矩形ABCD中,P是AD上一动点,O为BD的中点,连接PO并延长,交BC于点Q.
如图,在矩形ABCD中,P是AD上一动点,O为BD的中点,连接PO并延长,交BC于点Q.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
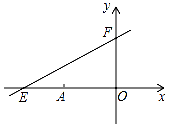 如图,直线y=kx+6与x、y轴分别交于E、F.点E坐标为(-8,0),点A的坐标为(-6,0),P(x,y)是直线y=kx+6上的一个动点.
如图,直线y=kx+6与x、y轴分别交于E、F.点E坐标为(-8,0),点A的坐标为(-6,0),P(x,y)是直线y=kx+6上的一个动点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com