
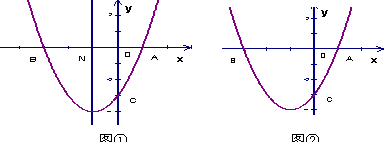
如图①, 已知抛物线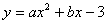 (a≠0)与
(a≠0)与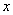 轴交于点A(1,0)和点B (-3,0),与y轴交于点C.
轴交于点A(1,0)和点B (-3,0),与y轴交于点C.
(1) 求抛物线的解析式;
(2) 设抛物线的对称轴与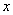 轴交于点N ,问在对称轴上是否存在点P,使△CNP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
轴交于点N ,问在对称轴上是否存在点P,使△CNP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
(3) 如图②,若点E为第三象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.
 |
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
已知线段a,b和∠1,
(1)请用尺规作一个三角形ABC,使BC=a,AC=b ,∠ACB=∠1
(2)在上题图中,若a=4,b=3,∠1=45º,请求出此三角形的面积。
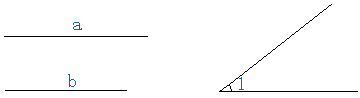
查看答案和解析>>
科目:初中数学 来源: 题型:
青少年“心理健康”问题已引起了全社会的关注,学校对此问题极为重视.对全校600名学生进行了一次“心理健康”知识测试,并从中抽取了部分学生的成绩(得分取正数,满分100分)作为样本,绘制了下面尚为完成的频率分布直方表。
| 分组 | 频数 | 频率 |
| 50.5~60.5 | 2 | 0.04 |
| 60.5~70.5 | 8 | 0.16 |
| 70.5~80.5 | 10 | |
| 80.5~90.5 | ||
| 90.5~100.5 | 0.28 | |
| 合计 | 1.00 |
请回答下列问题:
⑴填写频率分布直方表中的空格。
⑵若成绩在9 0分以上(不含90分)为优秀,试估计该校成绩优秀的有 人.
0分以上(不含90分)为优秀,试估计该校成绩优秀的有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
若有甲、乙两支水平相当的NBA球队需进行总决赛,一共需要打7场,前4场2比2,最后三场比赛,规定三局两胜者为胜方,如果在第一次比赛中甲获胜,这时乙最终取胜的可能性有多大?(不考虑主场优势)( )
A. B.
B. C.
C.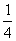 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示,在方格纸上建立的平面直角坐标系中,将△ABO绕点O按顺时针方向旋转90°,得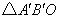 ,则点
,则点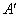 的坐标为( )
的坐标为( )
A.(3,1) B.(3,2) C.(2,3) D.(1,3)
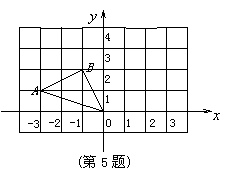 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知在等腰△ABC中,∠A=∠B=30°,过点C作CD⊥AC交AB于点D.
(1)尺规作图:过A,D,C三点作⊙O(只要求作出图形,保留痕迹,不要求写作法);
(2)求证:BC是过A,D,C三点的圆的切线;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com