
【题目】如图,点E在正方形ABCD的边AB上,连接DE,过点C作CF⊥DE于F,过点A作AG∥CF交DE于点G.
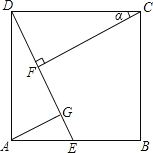
(1)求证:△DCF≌△ADG.
(2)若点E是AB的中点,设∠DCF=α,求sinα的值.
【答案】(1)证明见解析
(2)sinα=![]() 。
。
【解析】
试题分析:(1)由正方形的性质得AD=DC,∠ADC=90°,根据垂直的定义求出∠CFD=∠CFG=90°,再根据两直线平行,内错角相等求出∠AGD=∠CFG=90°,从而得到∠AGD=∠CFD,再根据同角的余角相等求∠ADG=∠DCF,然后利用“角角边”证明△DCF和△ADG全等即可。
(2)设正方形ABCD的边长为2a,表示出AE,再利用勾股定理列式求出DE,然后根据锐角的正弦等于对边比斜边求出∠ADG的正弦,即为α的正弦。
解:(1)证明:在正方形ABCD中,AD=DC,∠ADC=90°,
∵CF⊥DE,∴∠CFD=∠CFG=90°。
∵AG∥CF,∴∠AGD=∠CFG=90°。∴∠AGD=∠CFD。
又∵∠ADG+∠CDE=∠ADC=90°,∠DCF+∠CDE=90°,∴∠ADG=∠DCF。
∵在△DCF和△ADG中,∠AGD=∠CFD,∠ADG=∠DCF,AD=DC,
∴△DCF≌△ADG(AAS)。
(2)设正方形ABCD的边长为2a,
∵点E是AB的中点,∴AE=![]() ×2a=a。
×2a=a。
在Rt△ADE中,![]() ,
,
∴![]() 。
。
∵∠ADG=∠DCF=α,∴sinα=![]() 。
。


科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的对角线
的对角线![]() 交于点
交于点![]() ,直角三角形
,直角三角形![]() 绕点
绕点![]() 按逆时针旋转,
按逆时针旋转,![]()
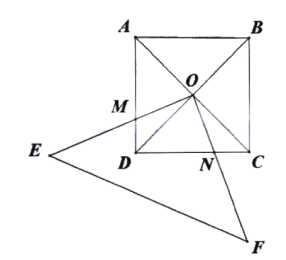
(1)若直角三角形绕点![]() 逆时针转动过程中分别交
逆时针转动过程中分别交![]() 两边于
两边于![]() 两点
两点
①求证:![]() ;
;
②连接![]() ,那么
,那么![]() 有什么样的关系?试说明理由
有什么样的关系?试说明理由
(2)若正方形的边长为2,则正方形![]() 与
与![]() 两个图形重叠部分的面积为多少?(不需写过程直接写出结果)
两个图形重叠部分的面积为多少?(不需写过程直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 ,在平面直角坐标系中,边长为 1 的正方形OA1B1C 的对角线 A1C 和OB1 交于点 M1,以 M1A1为对角线作第二个正方形 A2A1B2M1对角线 A1M1和 A2 B2 交于点 M 2 ;以 M 2 A1 为对角线作第三个正方形 A3 A1B3M 2,对角线 A1M 2 和 A3 B3 交于点 M 3 ;…,依此类推,那么 M 1 的坐标为_____;这样作的第 n 个正方形的对角线交点 Mn 的坐标为_____.
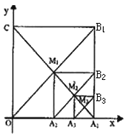
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知菱形ABCD的边长为5,∠DAB=60°.将菱形ABCD绕着A逆时针旋转得到菱形AEFG,设∠EAB=α,且0°<α<90°,连接DG、BE、CE、CF.
(1)如图(1),求证:△AGD≌△AEB;
(2)当α=60°时,在图(2)中画出图形并求出线段CF的长;
(3)若∠CEF=90°,在图(3)中画出图形并求出△CEF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】沾益区兴隆水果店计划用1000元购进甲、乙两种新出产的水果140千克,这两种水果的进价、售价如下表所示:
进价(元/千克) | 售价(元/千克) | |
甲 | 5 | 8 |
乙 | 9 | 13 |
(1)这两种水果各购进多少千克?
(2)该水果店全部销售完这批水果时获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
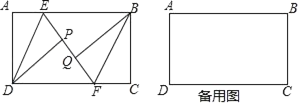
【题目】如图,在矩形ABCD中,AD=4,E,F分别为边AB,CD上一动点,AE=CF,分别以DE,BF为对称轴翻折△ADE,△BCF,点A,C的对称点分别为P,Q.若点P,Q,E,F恰好在同一直线上,且PQ=1,则EF的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
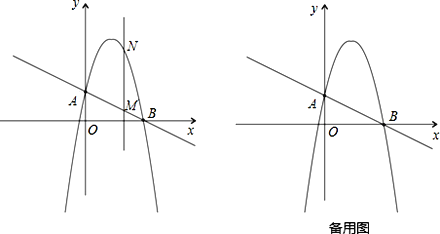
【题目】如图,一次函数![]() 分别交y轴、x 轴于A、B两点,抛物线
分别交y轴、x 轴于A、B两点,抛物线![]() 过A、B两点.
过A、B两点.
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于点M,交这个抛物线于点N.求当t 取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在下列横线上用含有![]() 的代数式表示相应图形的面积.
的代数式表示相应图形的面积.
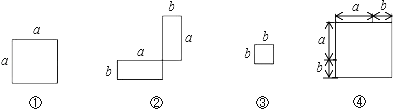
① ② ③ ④
(2)通过拼图,你发现前三个图形的面积与第四个图形面积之间有什么关系?请用数学式子表达: .
(3)利用(2)的结论计算![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
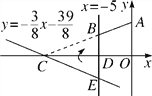
【题目】如图,在平面直角坐标系xOy中,A(0,5),直线x=-5与x轴交于点D,直线y=-![]() x-
x-![]() 与x轴及直线x=-5分别交于点C,E.点B,E关于x轴对称,连接AB.
与x轴及直线x=-5分别交于点C,E.点B,E关于x轴对称,连接AB.
(1)求点C,E的坐标及直线AB的解析式;
(2)若S=S△CDE+S四边形ABDO,求S的值;
(3)在求(2)中S时,嘉琪有个想法:“将△CDE沿x轴翻折到△CDB的位置,而△CDB与四边形ABDO拼接后可看成△AOC,这样求S便转化为直接求△AOC的面积,如此不更快捷吗?”但大家经反复验算,发现S△AOC≠S,请通过计算解释他的想法错在哪里.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com