
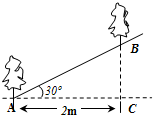
 如图,沿倾斜角为30°的山坡植树,要求相邻两棵树间的水平距离AC为2m,那么相邻两棵树的斜坡距离AB为( )m.
如图,沿倾斜角为30°的山坡植树,要求相邻两棵树间的水平距离AC为2m,那么相邻两棵树的斜坡距离AB为( )m.| A. | $\frac{4}{3}$$\sqrt{3}$ | B. | $\frac{2}{3}$$\sqrt{3}$ | C. | 1 | D. | 4 |
分析 AB是Rt△ABC的斜边,这个直角三角形中,已知一边和一锐角,满足解直角三角形的条件,可求出AB的长,
解答 解:在Rt△ABC中,∠C=90°,∠A=30°,AC=2m,
cos∠A=$\frac{AC}{AB}$,
∴cos30°=$\frac{2}{AB}$,
∴AB=$\frac{2}{cos30°}$=$\frac{2}{\frac{\sqrt{3}}{2}}$=$\frac{4}{3}\sqrt{3}$m,
故选:A.
点评 此题是解直角三角形的应用--坡度坡角问题,主要考查了特殊角的三角函数值,三角函数的定义,关键是设法化归为解直角三角形问题,必要时应添加辅助线,构造出直角三角形.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案科目:初中数学 来源: 题型:选择题
| A. | 134×107 | B. | 1.34×108 | C. | 1.34×109 | D. | 134×1010 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知抛物线的表达式为y=-x2+6x+c.
已知抛物线的表达式为y=-x2+6x+c.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ①②④ | C. | ①②⑤ | D. | ①②④⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
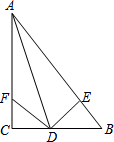 如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于点E,点F在AC上,BD=DF.
如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于点E,点F在AC上,BD=DF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com