

分析 根据相似三角形的性质定理得到∠B=∠B1,∠BAC=∠B1A1C1,根据相似三角形的判定定理证明△BAD∽△B1A1D1,根据相似三角形的性质定理得到答案.
解答 解:∵△ABC∽△A1B1C1,
∴∠B=∠B1,∠BAC=∠B1A1C1,
∵AD、A1D1分别是△ABC和△A1B1C1的角平分线,
∴∠BAD=∠B1A1D1,又∠B=∠B1,
∴△BAD∽△B1A1D1,
∴$\frac{AD}{{A}_{1}{D}_{1}}$=$\frac{AB}{{A}_{1}{B}_{1}}$=k.
点评 本题考查的是相似三角形的性质和判定,掌握相似三角形的判定定理是解题的关键,注意角平分线的定义的应用.


科目:初中数学 来源: 题型:填空题
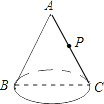 如图,有一个圆锥,它的底面半径是2cm,母线长是8cm,在点B处有一只蚂蚁,它想吃到与B点相对且离圆锥顶点3$\sqrt{2}$cm 的点P处的食物,蚂蚁爬行的最短路程是2$\sqrt{5}$cm.
如图,有一个圆锥,它的底面半径是2cm,母线长是8cm,在点B处有一只蚂蚁,它想吃到与B点相对且离圆锥顶点3$\sqrt{2}$cm 的点P处的食物,蚂蚁爬行的最短路程是2$\sqrt{5}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
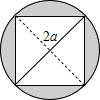 如图,直径为2a的圆中有一个正方形,那么阴影部分的面积为( )
如图,直径为2a的圆中有一个正方形,那么阴影部分的面积为( )| A. | (4-π)a2 | B. | (π-3)a2 | C. | (π-2.5)a2 | D. | (π-2)a2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某市对位于笔直公路AC上两个小区A、B的供水路线进行优化改造.供水站M在笔直公路AD上,测得供水站M在小区A的南偏东60°方向,在小区B的西南方向,小区A、B之间的距离为6米,求供水站M分别到小区A、B的距离.(结果保留根号)
某市对位于笔直公路AC上两个小区A、B的供水路线进行优化改造.供水站M在笔直公路AD上,测得供水站M在小区A的南偏东60°方向,在小区B的西南方向,小区A、B之间的距离为6米,求供水站M分别到小区A、B的距离.(结果保留根号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com