
【题目】如图,直线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,将一直角三角尺
,将一直角三角尺![]() 的直角顶点与点
的直角顶点与点![]() 重合,
重合,![]() 平分
平分![]() .
.
(1)![]() 的度数为______________
的度数为______________![]() ;
;
(2)将三角尺![]() 以每秒
以每秒![]() 的速度绕点
的速度绕点![]() 顺时针旋转,同时直线
顺时针旋转,同时直线![]() 也以每秒
也以每秒![]() 的速度绕点
的速度绕点![]() 顺时针旋转,设运动时间为
顺时针旋转,设运动时间为![]() 秒
秒![]() .
.
①求当![]() 为何值时,直线
为何值时,直线![]() 平分
平分![]() ;
;
②求当![]() 为何值时,直线
为何值时,直线![]() 平分
平分![]() .
.
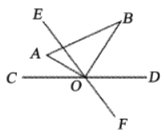
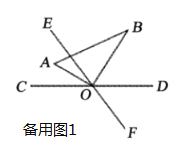
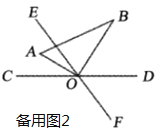
【答案】(1)60;(2)①t=2.5s或32.5s;②t=12s或36s.
【解析】
(1)根据角平分线的定义,即可求出∠COA,然后根据平角的定义即可求出![]() ;
;
(2)①根据直线EF平分∠AOB,分OE平分∠AOB和OF平分∠AOB两种情况,分别列出方程即可求出t;
②根据直线EF平分![]() ,分OE平分
,分OE平分![]() 和OF平分
和OF平分![]() 两种情况,分别列出方程即可求出t;
两种情况,分别列出方程即可求出t;
解:(1)∵![]() ,
,![]() 平分
平分![]()
∴∠COA=∠AOE=![]()
∵∠AOB=90°
∴![]() =180°-∠COA-∠AOB=60°
=180°-∠COA-∠AOB=60°
故答案为:60°;
(2)∠COF=180°-∠COE=120°
∴∠AOF=∠COE+∠AOC=150°
①直线EF平分∠AOB,分两种情况:
(i)当OE平分∠AOB时,∠AOE=45°,
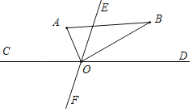
即9t+30°-3t=45°,
解得t=2.5;
(ii)当OF平分∠AOB时,∠AOF=45°,
即9t﹣150°﹣3t=45°,
解得t=32.5;
综上所述,当t=2.5s或32.5s时,直线EF平分∠AOB;
②直线EF平分∠BOD,分两种情况:
(i)当OE平分∠BOD时,∠BOE=![]() ∠BOD,
∠BOD,
即9t﹣60°﹣3t=![]() (60°﹣3t),
(60°﹣3t),
解得t=12;
当OF平分∠BOD时,∠DOF=![]() ∠BOD,
∠BOD,
即3t﹣(9t﹣240°)=![]() (3t﹣60°),
(3t﹣60°),
解得t=36;
综上所述,若直线EF平分∠BOD,t的值为12s或36s.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,平面直角坐标系中,矩形OABC的顶点A(6,0)、B(6,4),D是BC的中点.动点P从O点出发,以每秒1个单位的速度,沿着OA、AB、BD运动.设P点运动的时间为t秒(0<t<13).

(1)写出△POD的面积S与t之间的函数关系式,并求出△POD的面积等于9时点P的坐标;
(2)当点P在OA上运动时,连结CP.问:是否存在某一时刻t,当CP绕点P旋转时,点C能恰好落到AB的中点M处?若存在,请求出t的值并判断此时△CPM的形状;若不存在,请说明理由;
(3)当点P在AB上运动时,试探索当PO+PD的长最短时的直线PD的表达式。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接期末考试,某中学对全校七年级学生进行了一次数学摸底考试,并随机抽取了部分学生的测试成绩作为样本进行分析,绘制成了如图两幅不完整的统计图,请根据图中所给出的信息,解答下列问题:
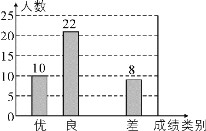

(1)在这次调查中,被抽取的学生的总人数为多少?
(2)请将表示成绩类别为“中”的条形统计图补充完整.
(3)在扇形统计图中,表示成绩类别为“优”的扇形所对应的圆心角的度数是多少?
(4)学校七年级共有1000人参加了这次数学考试,估计该校七年级共有多少名学生的数学成绩可以达到优秀.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程![]()
解:方程两边同时乘以(x+2)(x-2)…(A)
(x+2)(x-2)![]()
化简得:x-2+4x=2(x+2)….. (B)
去括号、移项得:x+4x-2x=4+2…(C)
解得:x=2…..(D)
原方程的解是x=2….(E)
问题:①上述解题过程的错误在第____步,其原因是_____②该步改正为:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3)。双曲线![]() 的图像经过BC的中点D,且与AB交于点E,连接DE。
的图像经过BC的中点D,且与AB交于点E,连接DE。

(1)求k的值及点E的坐标;
(2)若点F是边上一点,且△FBC∽△DEB,求直线FB的解析式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD是平行四边形,P是CD上的一点,且AP和BP分别分别平分∠DAB和∠CBA,QP∥AD,交AB于点Q.
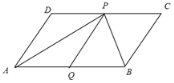
(1)求证:AP⊥PB;
(2)如果AD=5cm,AP=8cm,那么□ ABCD 的面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
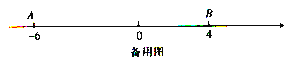
【题目】如图,数轴上点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为4,点
表示的数为4,点![]() 从点
从点![]() 出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点
出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度向左匀速运动.设运动的时间为
出发,以每秒2个单位长度的速度向左匀速运动.设运动的时间为![]()
![]() .
.
(1)当![]() 为何值时,
为何值时,![]() 、
、![]() 两点相遇?并写出相遇点所表示的数.
两点相遇?并写出相遇点所表示的数.
(2)当![]() 为何值时,
为何值时,![]() ?
?
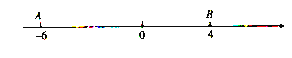
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市有两家出租车公司,收费标准不同,甲公司收费标准为:起步价8元,超过3千米后,超过的部分按照每千米1.5元收费;乙公司收费标准为:起步价11元,超过3千米后,超过的部分按照每千米1.2元收费,车辆行驶![]() 千米,本题中
千米,本题中![]() 取整数,不足1千米的路程按1千米计费,根据上述内容,完成以下问题:
取整数,不足1千米的路程按1千米计费,根据上述内容,完成以下问题:
(1)当![]() 时,乙公司比甲公司贵______元;
时,乙公司比甲公司贵______元;
(2)当![]() ,且
,且![]() 为整数时,甲乙两公司的收费分别是多少?(结果用化简后的含
为整数时,甲乙两公司的收费分别是多少?(结果用化简后的含![]() 的式子表示);
的式子表示);
(3)当行驶路程为18千米时,哪家公司的费用更便宜?便宜多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
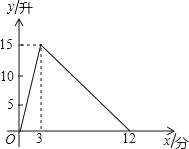
【题目】一个有进水管与出水管的容器,从某时刻开始的3分内只进水不出水,在随后的9分内既进水又出水,每分的进水量和出水量都是常数.容器内的水量y(单位:升)与时间x(单位:分)之间的关系如图所示.
①当0≤x≤3时,求y与x之间的函数关系.
②3<x≤12时,求y与x之间的函数关系.
③当容器内的水量大于5升时,求时间x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com