
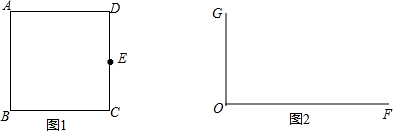
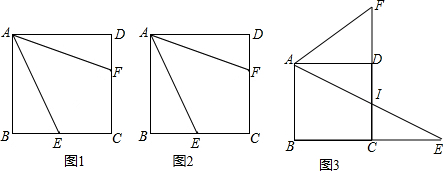
分析 利用题目提示直接画出图形,
(1)先利用勾股定理求出BE,再用作图即可求出CG,
(2)求出CG:BG,即可得出结论,判断出结论;
(3)借助小明的作出的线段,再借助线段的长度,即可作出图形.
解答 解:补全小明的图形如图1所示,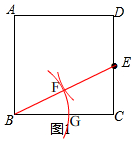
(1)∵正方形的边长为2,
∴BC=CD=2,
∵点E是CD中点,
∴CE=$\frac{1}{2}$CD=1,
在Rt△BCE中,BE=$\sqrt{B{C}^{2}+C{E}^{2}}$=$\sqrt{5}$,
由作图知,EF=CE=1,
∴BF=BE-EF=$\sqrt{5}$-1,
由作图知,BG=BF=$\sqrt{5}$-1,
∴CG=BC-BG=3-$\sqrt{5}$,
(2)由(1)知,BG=$\sqrt{5}$-1,CG=3-$\sqrt{5}$,
∴$\frac{CG}{BG}=\frac{3-\sqrt{5}}{\sqrt{5-1}}$=$\frac{\sqrt{5}-1}{2}$,
∴CG,BG的比是黄金比;
(3)如图2所示,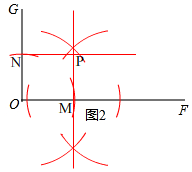
点评 此题是四边形综合题,主要考查了基本作图,勾股定理,线段的比,解本题的关键是掌握几种基本作图,是一道比较简单的综合题.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
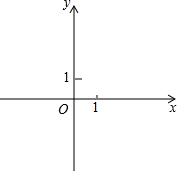 在平面直角坐标系xOy中,抛物线y=-x2+mx+n与x轴交于点A,B(A在B的左侧).
在平面直角坐标系xOy中,抛物线y=-x2+mx+n与x轴交于点A,B(A在B的左侧).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com