
”¾ĢāÄæ”æ”÷ABCĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬”ĻABC=90”ć£¬µćDŌŚAB±ßÉĻ£Ø²»ÓėµćA”¢BÖŲŗĻ£©£¬ŅŌCDĪŖŃü×÷µČŃüÖ±½Ē”÷CDE£¬”ĻDCE=90”ć£®
£Ø1£©ČēĶ¼1£¬×÷EF”ĶBCÓŚF£¬ĒóÖ¤£ŗ”÷DBC”Õ”÷CFE£»
£Ø2£©ŌŚĶ¼1ÖŠ£¬Į¬½ÓAE½»BCÓŚM£¬Ēó![]() µÄÖµ£»
掙术
£Ø3£©ČēĶ¼2£¬¹żµćE×÷EH”ĶCE½»CBµÄŃÓ³¤ĻßÓŚµćH£¬¹żµćD×÷DG”ĶDC£¬½»ACÓŚµćG£¬Į¬½ÓGH£®µ±µćDŌŚ±ßABÉĻŌĖ¶ÆŹ±£¬Ź½×Ó![]() µÄÖµ»į·¢Éś±ä»ÆĀš£æČō²»±ä£¬Ēó³öøĆÖµ£»Čō±ä»ÆĒėĖµĆ÷ĄķÓÉ£®
µÄÖµ»į·¢Éś±ä»ÆĀš£æČō²»±ä£¬Ēó³öøĆÖµ£»Čō±ä»ÆĒėĖµĆ÷ĄķÓÉ£®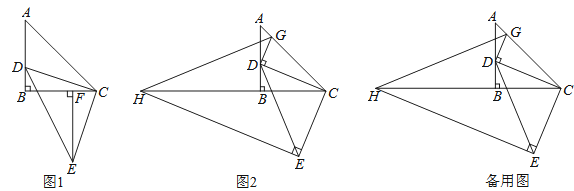
”¾“š°ø”æ£Ø1£©Ö¤Ć÷£ŗ”ß”÷CDEĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬”ĻDCE=90”ć£®
”ąCD=CE£¬”ĻDCB+”ĻECF=90”ć£¬
”ßEF”ĶBC£¬
”ą”ĻECF+”ĻCEF=90”ć£¬
”ą”ĻDCB=”ĻCEF£¬
ŌŚ”÷DBCŗĶ”÷CEFÖŠ£¬ £¬
£¬
”ą”÷DBC”Õ”÷CFE£»
£Ø2£©½ā£ŗČēĶ¼1£¬
”ß”÷DBC”Õ”÷CFE£¬
”ąBD=CF£¬BC=EF£¬
”ß”÷ABCĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬
”ąAB=BC£¬
”ąAB=EF£¬AD=BF£¬
ŌŚ”÷ABMŗĶ”÷EFMÖŠ£¬ £¬
£¬
”ą”÷ABM”Õ”÷EFM£¬
”ąBM=FM£¬
”ąBF=2BM£¬
”ąAD=2BM£¬
”ą![]() µÄÖµĪŖ2£»
µÄÖµĪŖ2£»
£Ø3£©½ā£ŗ![]() µÄÖµ²»±ä£®
µÄÖµ²»±ä£®
ŌŚEHÉĻ½ŲČ”EQ=DG£¬ČēĶ¼2£¬
ŌŚ”÷CDGŗĶ”÷CEQÖŠ £¬
£¬
”ą”÷CDG”Õ”÷CEQ£¬
”ąCG=CQ£¬”ĻDCG=”ĻECQ£¬
”ß”ĻDCG+”ĻDCB=45”ć£¬
”ą”ĻECQ+”ĻDCB=45”ć£¬
¶ų”ĻDCE=90”ć£¬
”ą”ĻHCQ=45”ć£¬
”ą”ĻHCQ=”ĻHCG£¬
ŌŚ”÷HCGŗĶ”÷HCQÖŠ£¬ £¬
£¬
”ą”÷HCG”Õ”÷HCQ£¬
”ąHG=HQ£¬
”ą![]() =
=![]() =1£®
=1£®
”¾½āĪö”æ£Ø1£©øł¾ŻµČŃüÖ±½ĒČż½ĒŠĪµÄŠŌÖŹµĆµ½CD=CE£¬ŌŁĄūÓĆµČ½ĒµÄÓą½ĒĻąµČµĆµ½”ĻDCB=”ĻCEF£¬Č»ŗóøł¾Ż”°AAS”±æÉÖ¤Ć÷”÷DBC”Õ”÷CFE£»
£Ø2£©ÓÉ”÷DBC”Õ”÷CFEµĆµ½BD=CF£¬BC=EF£¬ŌŁĄūÓĆ”÷ABCĪŖµČŃüÖ±½ĒČż½ĒŠĪµĆµ½AB=BC£¬ĖłŅŌAB=EF£¬AD=BF£¬½Ó×ÅÖ¤Ć÷”÷ABM”Õ”÷EFM£¬µĆµ½BM=FM£¬ĖłŅŌ![]() =2£»
=2£»
£Ø3£©ŌŚEHÉĻ½ŲČ”EQ=DG£¬ČēĶ¼2£¬ĻČÖ¤Ć÷”÷CDG”Õ”÷CEQµĆµ½CG=CQ£¬”ĻDCG=”ĻECQ£¬ÓÉÓŚ”ĻDCG+”ĻDCB=45”ć£¬Ōņ”ĻECQ+”ĻDCB=45”ć£¬ĖłŅŌ”ĻHCQ=45”ć£¬ŌŁÖ¤Ć÷”÷HCG”Õ”÷HCQ£¬ŌņµĆµ½HG=HQ£¬Č»ŗóæɼĘĖć³ö![]() =1£®
=1£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌ¤¼ĘĻĀ½ģŹĄ²©»į½«ĪüŅżŌ¼69 000 000ČĖ“Ī²Ī¹Ū£®½«69 000 000ÓĆæĘѧ¼ĒŹż·Ø±ķŹ¾ÕżČ·µÄŹĒ£Ø £©
A.0.69”Į108
B.6.9”Į106
C.6.9”Į107
D.69”Į106
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬”÷AOBÖŠ£¬A£Ø£8£¬0£©£¬B£Ø0£¬ ![]() £©£¬ACĘ½·Ö”ĻOAB£¬½»yÖįÓŚµćC£¬µćPŹĒxÖįÉĻŅ»µć£¬”ŃP¾¹żµćA”¢C£¬ÓėxÖįÓŚµćD£¬¹żµćC×÷CE”ĶAB£¬“¹×ćĪŖE£¬ECµÄŃÓ³¤Ļß½»xÖįÓŚµćF£¬
£©£¬ACĘ½·Ö”ĻOAB£¬½»yÖįÓŚµćC£¬µćPŹĒxÖįÉĻŅ»µć£¬”ŃP¾¹żµćA”¢C£¬ÓėxÖįÓŚµćD£¬¹żµćC×÷CE”ĶAB£¬“¹×ćĪŖE£¬ECµÄŃÓ³¤Ļß½»xÖįÓŚµćF£¬
£Ø1£©”ŃPµÄ°ė¾¶ĪŖ””””””””£»
£Ø2£©ĒóÖ¤£ŗEFĪŖ”ŃPµÄĒŠĻߣ»
£Ø3£©ČōµćHŹĒ![]() ÉĻŅ»¶Æµć£¬Į¬½ÓOH”¢FH£¬µ±µćHŌŚ
ÉĻŅ»¶Æµć£¬Į¬½ÓOH”¢FH£¬µ±µćHŌŚ![]() ÉĻŌĖ¶ÆŹ±£¬ŹŌĢ½¾æ
ÉĻŌĖ¶ÆŹ±£¬ŹŌĢ½¾æ![]() ŹĒ·ńĪŖ¶ØÖµ£æČōĪŖ¶ØÖµ£¬ĒóĘäÖµ£»Čō²»ŹĒ¶ØÖµ£¬ĒėĖµĆ÷ĄķÓÉ.
ŹĒ·ńĪŖ¶ØÖµ£æČōĪŖ¶ØÖµ£¬ĒóĘäÖµ£»Čō²»ŹĒ¶ØÖµ£¬ĒėĖµĆ÷ĄķÓÉ.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŖĮĖ½āÕć½Ź”֊ѧɜµÄÉķĢåĖŲÖŹĒéæö£¬Ó¦²ÉÓĆ____µ÷²é£®(Ń”Ģī”°Č«Ćę”±»ņ”°³éŃł”±)
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”潫Ņ»øöČż½ĒŠĪ·Å“óĪŖÓėĖüĻąĖʵÄČż½ĒŠĪ£¬Čē¹ūÖܳ¤Ą©“óĪŖŌĄ“µÄ3±¶£¬ÄĒĆ“Ć껿Ą©“óĪŖŌĄ“µÄ£Ø””””£©
A. 3±¶B. 9±¶C. 18±¶D. 81±¶
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ĮāŠĪOBCDµÄ±ßOBŌŚxÖįÉĻ£¬·“±ČĄżŗÆŹży=![]() £Øx£¾0£©µÄĶ¼Ļó¾¹żĮāŠĪ¶Ō½ĒĻߵĽ»µćA£¬ĒŅÓė±ßBC½»ÓŚµćF£¬µćAµÄ×ų±źĪŖ£Ø4£¬2£©£®ŌņµćFµÄ×ų±źŹĒ_________________
£Øx£¾0£©µÄĶ¼Ļó¾¹żĮāŠĪ¶Ō½ĒĻߵĽ»µćA£¬ĒŅÓė±ßBC½»ÓŚµćF£¬µćAµÄ×ų±źĪŖ£Ø4£¬2£©£®ŌņµćFµÄ×ų±źŹĒ_________________

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¹Ū²ģĻĀĮŠø÷Ź½:¢Łabx-adx£»¢Ś2x![]() y+6xy
y+6xy![]() £»¢Ū8m
£»¢Ū8m![]() -4m
-4m![]() +2m+1£»¢Üa
+2m+1£»¢Üa![]() +a
+a![]() b+ab
b+ab![]() -b
-b![]() £»¢Ż(p+q)x
£»¢Ż(p+q)x![]() y-5x
y-5x![]() (p+q)+6(p+q)
(p+q)+6(p+q) ![]() £»¢Ža
£»¢Ža![]() (x+y)(x-y)-4b(y+x).ĘäÖŠæÉŅŌÓĆĢį¹«ŅņŹ½·Ø·Ö½āŅņŹ½µÄŹĒ(””””)
(x+y)(x-y)-4b(y+x).ĘäÖŠæÉŅŌÓĆĢį¹«ŅņŹ½·Ø·Ö½āŅņŹ½µÄŹĒ(””””)
A.¢Ł¢Ś¢Ż
B.¢Ś¢Ü¢Ż
C.¢Ś¢Ü¢Ž
D.¢Ł¢Ś¢Ż¢Ž
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĮŠŌĖĖć½į¹ūÕżČ·µÄŹĒ£Ø £©
A.a3+a2=a5
B.£Øx+y£©2=x2+y2
C.x8”Āx2=x4
D.£Øab£©2=a2b2
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com