
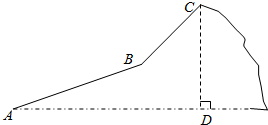
 小明春游,登了一座山,地形险峻.由山脚A沿坡角为30°的山坡AB行走480米,到达一个景点B,再由B地沿山坡BC行走360米到达山顶C.如果在山顶C处观测到景点B的俯角为45°,小明在想:山高CD是多少米,你能得出答案吗?(保留$\sqrt{2}$)
小明春游,登了一座山,地形险峻.由山脚A沿坡角为30°的山坡AB行走480米,到达一个景点B,再由B地沿山坡BC行走360米到达山顶C.如果在山顶C处观测到景点B的俯角为45°,小明在想:山高CD是多少米,你能得出答案吗?(保留$\sqrt{2}$) 分析 过B作BE⊥AD于点D,作BF⊥CD于点F,在直角△ABE中,利用三角函数求得BE的长,在直角△BCF中利用三角函数求得CF的长,则CD=BE+CF,据此即可求解.
解答  解:过B作BE⊥AD于点D,作BF⊥CD于点F.
解:过B作BE⊥AD于点D,作BF⊥CD于点F.
在直角△ABE中,∠A=30°,则BE=$\frac{1}{2}$AB=$\frac{1}{2}$×480=240(米);
在直角△BCF中,∠CBF=45°,则CF=BC•sin45°=360×$\frac{\sqrt{2}}{2}$=180$\sqrt{2}$(米).
则CD=CF+DF=CF+BE=240+180$\sqrt{2}$米.
答:山高CD是(240+180$\sqrt{2}$)米.
点评 本题考查仰角的定义,能借助仰角构造直角三角形并解直角三角形是关键.


科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若a>b,则$\frac{1}{a}$<$\frac{1}{b}$ | B. | 若a>b,则a2>b2 | C. | 若a>b,则1-a<1-b | D. | 若a>b,ac2>bc2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com