
 如图,AB是⊙O的直径,C为⊙O上一点,过点B作经过点C的直线CD的垂线,垂足为E (即BE⊥CD),BE交⊙O于点F,且BC平分∠ABE.
如图,AB是⊙O的直径,C为⊙O上一点,过点B作经过点C的直线CD的垂线,垂足为E (即BE⊥CD),BE交⊙O于点F,且BC平分∠ABE.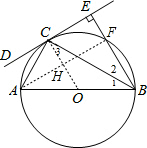 (1)证明:连结OC,如图,
(1)证明:连结OC,如图,| OA2-AH2 |


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源: 题型:
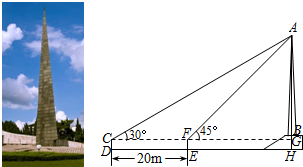 苏中七战七捷纪念馆位于江苏海安县城中心,馆内纪念碑碑身造型似一把刺刀矗立在广袤的苏中大地上,堪称世界之最,被誉为“天下第一刺刀”.如图,在一次数学课外实践活动中,老师要求测纪念碑碑身的高度AB,小明在D处用高1.5m测角仪CD,测得纪念碑碑身顶端A的仰角为30°,然后向纪念碑碑身前进20m到达E处,又测得纪念碑碑身顶端A的仰角为45°,已知纪念碑碑身下面的底座高度BH为1.8m.求纪念碑碑身的高度AB(结果精确到个位,参考数据:
苏中七战七捷纪念馆位于江苏海安县城中心,馆内纪念碑碑身造型似一把刺刀矗立在广袤的苏中大地上,堪称世界之最,被誉为“天下第一刺刀”.如图,在一次数学课外实践活动中,老师要求测纪念碑碑身的高度AB,小明在D处用高1.5m测角仪CD,测得纪念碑碑身顶端A的仰角为30°,然后向纪念碑碑身前进20m到达E处,又测得纪念碑碑身顶端A的仰角为45°,已知纪念碑碑身下面的底座高度BH为1.8m.求纪念碑碑身的高度AB(结果精确到个位,参考数据:| 2 |
| 3 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图是一个圆形人工湖的示意图,弦AB是湖上的一座桥,已知桥AB长100m,测得圆周角∠ACB=60°,则这个人工湖的直径AD为( )
如图是一个圆形人工湖的示意图,弦AB是湖上的一座桥,已知桥AB长100m,测得圆周角∠ACB=60°,则这个人工湖的直径AD为( )A、
| ||||
B、
| ||||
C、100
| ||||
| D、150m |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2×5 |
| 3 |
| 12 |
| xy |
|
| 288 |
|
| 6 |
| 10 |
| 225 |
| 4y |
| 16ab2c3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在直角坐标系中,点A、B的坐标分别为(1,3)和(2,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是
如图,在直角坐标系中,点A、B的坐标分别为(1,3)和(2,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com