练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】一条开口向下的抛物线的顶点坐标是（2，3），则这条抛物线有（ ）
    A.最大值3
    B.最小值3
    C.最大值2
    D.最小值﹣2

    【答案】A
    【解析】解：∵抛物线开口向下， ∴二次函数有最大值，
    当x=2时，二次函数值最大，最大值为3．
    故选A．
    【考点精析】关于本题考查的二次函数的性质，需要了解增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小才能得出正确答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】ABCD中，E是CD边上一点，
    （1）将△ADE绕点A按顺时针方向旋转，使AD、AB重合，得到△ABF，如图1所示．观察可知：与DE相等的线段是 ， ∠AFB=∠ .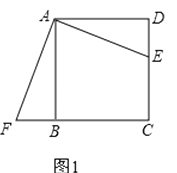
    （2）如图2，正方形ABCD中，P、Q分别是BC、CD边上的点，且∠PAQ=45°，试通过旋转的方式说明：DQ+BP=PQ.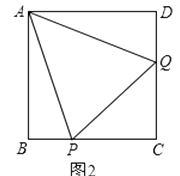
    （3）在（2）题中，连接BD分别交AP、AQ于M、N，你还能用旋转的思想说明BM2+DN2=MN2 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠C=90 ，AC=BC，AD平分∠CAB，交BC于D，DE⊥AB于E，且AB=6cm，则△BED的周长是cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

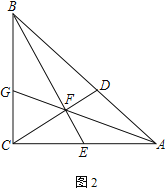
    【题目】△ABC中，∠ACB＝90°，点E为AC的中点，CD⊥BE交AB于D点，交BE于点F

    (1) 如图1，若AC＝2BC，求证：AD＝2BD

    (2) 如图2，若∠ACD＝30°，连AF并延长交BC于G点，求的值

    (3) 在(1)的条件下，若AC＝4，以AB为边作等腰直角三角形ABM（点M与点C在AB异侧），直接写出CM的长

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】H7N9型禽流感是一种新型禽流感，于2013年3月底在上海和安徽两地率先发现．H7N9型禽流感是全球首次发现的新亚型流感病毒，其细胞的直径约为0.000000106m，用科学记数法表示这个数是（ ）
    A.0.106×10﹣6m
    B.0.106×106m
    C.1.06×10﹣7m
    D.1.06×107m

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图表示两辆汽车行驶路程与时间的关系（汽车B在汽车A后出发）的图象，试回答下列问题：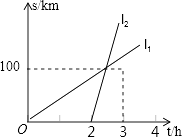

    （1）图中l1 ， l2分别表示哪一辆汽车的路程与时间的关系？
    （2）写出汽车A和汽车B行驶的路程s与时间t的函数关系式，并求汽车A和汽车B的速度；
    （3）图中交点的实际意义是什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某运动队欲从甲、乙两名优秀选手中选一名参加全省射击比赛，该运动队预先对这两名选手进行了8次测试，测得的成绩如表：

    次数

    选手甲的成绩（环）

    选手乙的成绩（环）

    1

    9.6

    9.5

    2

    9.7

    9.9

    3

    10.5

    10.3

    4

    10.0

    9.7

    5

    9.7

    10.5

    6

    9.9

    10.3

    7

    10.0

    10.0

    8

    10.6

    9.8

    根据统计的测试成绩，请你运用所学过的统计知识作出判断，派哪一位选手参加比赛更好？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线y=ax2+bx+c（a＞0）与x轴的两个交点分别为A（﹣1，0）、B（3，0），与y 轴的交点为点D，顶点为C，

    （1）写出该抛物线的对称轴方程；

    （2）当点C变化，使60°≤∠ACB≤90°时，求出a的取值范围；

    （3）作直线CD交x轴于点E，问：在y轴上是否存在点F，使得△CEF是一个等腰直角三角形？若存在，请求出a的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园，其中一边靠墙，另外三边周长为30米的篱笆围成．已知墙长为18米(如右图所示)，设这个苗圃园垂直于墙的一边长为x米．

    ⑴若苗圃园的面积为72平方米，求x；

    ⑵若平行于墙的一边长不小于8米，这个苗圃园的面积有最大值和最小值吗？如果有，求出最大值和最小值；如果没有，请说明理由；

    ⑶当这个苗圃园的面积不小于100平方米时，直接写出x的取值范围．

    查看答案和解析>>

    同步练习册答案