
【题目】如图,在Rt△ABC中,∠A=90°, ∠B=30°,BC=![]() +1,点E、F分别是BC、AC边上的动点,沿EF所在直线折叠∠C,使点C的对应点C′始终落在边AB上,若△BEC′是直角三角形时,则BC′的长为_____________.
+1,点E、F分别是BC、AC边上的动点,沿EF所在直线折叠∠C,使点C的对应点C′始终落在边AB上,若△BEC′是直角三角形时,则BC′的长为_____________.

【答案】![]() 或2
或2
【解析】分析:分两种情况:①当∠BEC′=90°时,设EC′=x,则BE=![]() x,BC′=2x,EC=x,由BC=BE+EC,可求出x的值,即可得到结论;
x,BC′=2x,EC=x,由BC=BE+EC,可求出x的值,即可得到结论;
②当∠BC′E=90°时,设EC′=x,则BE=2x,BC′=![]() x,EC=x,由BC=BE+EC,可求出x的值,即可得到结论.
x,EC=x,由BC=BE+EC,可求出x的值,即可得到结论.
详解:分两种情况:①当∠BEC′=90°时,设EC′=x,则BE=![]() x,BC′=2x,EC=x,∴BC=BE+EC=
x,BC′=2x,EC=x,∴BC=BE+EC=![]() x+x=
x+x=![]() +1,解得:x=1,∴BC′=2x=2;
+1,解得:x=1,∴BC′=2x=2;
②当∠BC′E=90°时,设EC′=x,则BE=2x,BC′=![]() x,EC=x,∴BC=BE+EC=2x+x=
x,EC=x,∴BC=BE+EC=2x+x=![]() +1,解得:x=
+1,解得:x=![]() ,∴BC′=
,∴BC′=![]() x=
x=![]() .
.
故答案为:![]() 或2.
或2.


科目:初中数学 来源: 题型:
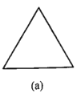
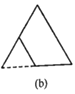
【题目】如图所示,图(a)是一块边长为1,周长记为![]() 的正三角形纸板,沿图(a)的底边剪去一块边长为
的正三角形纸板,沿图(a)的底边剪去一块边长为![]() 的正三角形纸板后得到图(b),然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的
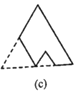
的正三角形纸板后得到图(b),然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的![]() 后,得图(c),(d),……,记第
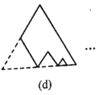
后,得图(c),(d),……,记第![]() )块纸板的周长为Pn.则
)块纸板的周长为Pn.则![]() ____;
____;![]() _______.
_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下面的表格中,从左到右依次在每个小方格中填入一个数,使得其中任意三个相邻方格中所填数之和都相等,例如:![]() .
.
第1格 | 第2格 | 第3格 | 第4格 | 第5格 | 第6格 | 第7格 | 第8格 | 第9格 | … | 第n格 |
8 |
|
|
| -2 | _____ | _____ | _____ | -3 | … | _____ |
(1)求出第4格中的数![]() ;
;
(2)第6格中的数是 (直接填具体数);
(3)前2020个格子中所填各数之和为 (直接填空).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直角梯形OABC中,BC∥OA,OA=6,BC=2,∠BAO=45°.
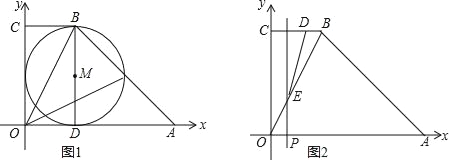
(1)OC的长为 ;
(2)D是OA上一点,以BD为直径作⊙M,⊙M交AB于点Q.当⊙M与y轴相切时,sin∠BOQ= ;
(3)如图2,动点P以每秒1个单位长度的速度,从点O沿线段OA向点A运动;同时动点D以相同的速度,从点B沿折线B﹣C﹣O向点O运动.当点P到达点A时,两点同时停止运动.过点P作直线PE∥OC,与折线O﹣B﹣A交于点E.设点P运动的时间为t(秒).求当以B、D、E为顶点的三角形是直角三角形时点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】7张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
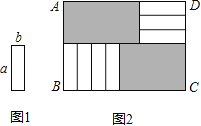
A.a=![]() bB.a=3bC.a=
bB.a=3bC.a=![]() bD.a=4b
bD.a=4b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】望江中学为了了解学生平均每天“诵读经典”的时间,在全校范围内随机抽查了部分学生进行调查统计,并将调查统计的结果分为:每天诵读时间t≤20分钟的学生记为A类,20分钟<t≤40分钟的学生记为B类,40分钟<t≤60分钟的学生记为C类,t>60分钟的学生记为D类四种.将收集的数据绘制成如下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
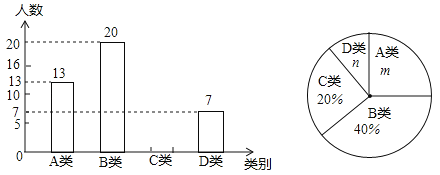
(1)m=%,n=%,这次共抽查了名学生进行调查统计;
(2)请补全上面的条形统计图;
(3)如果该校共有1200名学生,请你估计该校C类学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某学校教学楼AB的后面有一建筑物CD,在距离CD正后方28米的观测点P处,以22°的仰角测得建筑物的顶端C恰好挡住教学楼的顶端A,而在建筑物CD上距离地面2米高的E处,测得教学楼的顶端A的仰角为45°,求教学楼AB的高度(结果保留整数).
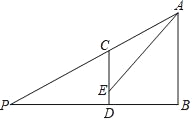
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC中,∠ABC=90°,以AB为直径作⊙O交AC边于点D,E是边BC的中点,连接DE,OD.
(Ⅰ)如图①,求∠ODE的大小;
(Ⅱ)如图②,连接OC交DE于点F,若OF=CF,求∠A的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)四边形ABCD中,已知∠ABC+∠ADC=180°,AB=AD,DA⊥AB,点E在CD的延长线上,∠BAC=∠DAE.
(1)求证:△ABC≌△ADE;
(2)求证:CA平分∠BCD;
(3)如图(2),设AF是△ABC的BC边上的高,求证:EC=2AF.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com