
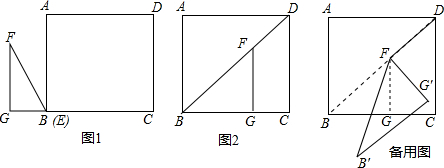
���� ��1�����þ��ε����ʺ��ɶ�����FG���������������ε����ʿɵ�BG�ij���
��2������ͼ1����0��t��2ʱ�����������ε������ʽ��ý��ۣ�����ͼ2����2��t��10ʱ�����������ε������ʽ���ɵõ����ۣ�����ͼ3����10��t��12ʱ�������������ε������ɵõ����ۣ�
��3���ɵڣ�1����֪��BG=$\frac{16}{3}$�����ǵõ�BF=$\frac{20}{3}$���� BM=BNʱ����ͼ4�����ݵ��������ε����ʵõ���M=��BNM�����ڡ�FBG=��M+��BNM=2��M���õ���M=��M FB?�����ǵõ�B?M=B?F=$\frac{20}{3}$�����ݹ��ɶ�����ý������ͼ5�����ݵ��������ε����ʵõ���M=��BNM�����ڡ�FB?G?=��FBG�����ǵõ���M=��M FB?=��BNM���õ�B?M=B?F=$\frac{20}{3}$�����ɵõ����ۣ��� NM=NBʱ����ͼ6�����ݵ��������ε����ʵõ���M=��NBM�����ڡ�FB?G?=��FBG�����ǵõ���M=��FB?G?��FM=FB?=$\frac{20}{3}$���� MN=MBʱ����ͼ7�����ݵ��������ε����ʡ�N=��NBM�����ڡ�FB?G?=��FBG���õ���N=��FB?G?���õ�FB?��BN�����ǵõ�B?M=FM�����ݹ��ɶ������ɵõ������
���  �⣺��1���ھ���ABCD�У�AB=6��BD=10��
�⣺��1���ھ���ABCD�У�AB=6��BD=10��
���ɹ��ɶ�����BC=8��
����Rt��EFG��GE+AB=BC��FG=2GE��
��FG=4��
����Fǡ�þ���BDʱ��
�ߡ�FGE=90�㣬��C=90��
��FG��DC��
���BFG�ס�BCD��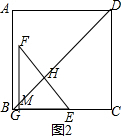
��$\frac{FG}{DC}=\frac{BG}{BC}$����$\frac{4}{6}$=$\frac{BG}{8}$��
��BG=$\frac{16}{3}$��
��BE=$\frac{22}{3}$��
�൱��Fǡ�þ���BDʱ��t=$\frac{22}{3}$��
��2������ͼ1����0��t��2ʱ��S=$\frac{3}{11}$t2��
����ͼ2����2��t��$\frac{22}{3}$ʱ��S=-$\frac{9}{88}$t2+$\frac{3}{2}$t-$\frac{3}{2}$��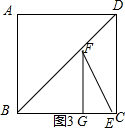
����ͼ3����$\frac{22}{3}$��t��8ʱ��S=4��
����ͼ4����8��t��10ʱ��S=-t2+16t-60��
����������S=$\left\{\begin{array}{l}{\frac{3}{11}{t}^{2}��0��t��2��}\\{-\frac{9}{88}{t}^{2}+\frac{3}{2}t-\frac{3}{2}��2��t��\frac{22}{3}��}\\{4��\frac{22}{3}��t��8��}\\{-{t}^{2}+16t-60��8��t��10��}\end{array}\right.$��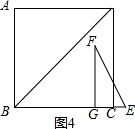
��3���ɵڣ�1����֪��BG=$\frac{16}{3}$��
��BF=$\frac{20}{3}$
�� BM=BNʱ����ͼ4��
���M=��BNM��
�ߡ�FBG=��M+��BNM=2��M��
��FB?G?=��FBG��
��FBG=��M+��M FB?��
���M=��M FB?��
��B?M=B?F=$\frac{20}{3}$��
��M G?=$\frac{20}{3}$+$\frac{16}{3}$=12��
��$MF=\sqrt{{{12}^2}+{4^2}}=4\sqrt{10}$��
��ͼ5�����M=��BNM��
�ߡ�FB?G?=��FBG��
���M=��M FB?=��BNM��
��B?M=B?F=$\frac{20}{3}$��
��B?M=B?F=$\frac{20}{3}$��
��M G?=$\frac{20}{3}$-$\frac{16}{3}$=$\frac{4}{3}$��
��Rt��G?FM�У��ɹ��ɶ����ã�$MF=\sqrt{{{��\frac{4}{3}��}^2}+{4^2}}=\frac{4}{3}\sqrt{10}$��
�� NM=NBʱ����ͼ6��
���M=��NBM��
�ߡ�FB?G?=��FBG��
���M=��FB?G?��
��FM=FB?=$\frac{20}{3}$��
�� MN=MBʱ����ͼ7��
���N=��NBM��
�ߡ�FB?G?=��FBG��
���N=��FB?G?��
��FB?��BN��
��B?M=FM��
����B?M=FM=x��
��${x^2}={4^2}+{��\frac{16}{3}-x��^2}$��
��$x=\frac{25}{6}$��
��FM=$\frac{25}{6}$��
������������FM=$4\sqrt{10}$��$\frac{4}{3}\sqrt{10}$��$\frac{20}{3}$��$\frac{25}{6}$ʱ����BMNΪ���������Σ�
���� ���⿼���˼��α任�����ɶ��������ε����ʣ����������ε����ʣ����������ε��ж������ʣ������Ľ���ʽ����ȷ�Ļ���ͼ���ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
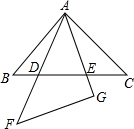 ������ȫ�ȵĵ���ֱ�������ΰڳ���ͼ��ʾ�����ӣ�ͼ�е����е㣬�߶���ͬһƽ���ڣ�������ͼ���ҳ��������ƶ���ȫ�ȵ������Σ���˵���������Ƶ����ɣ�
������ȫ�ȵĵ���ֱ�������ΰڳ���ͼ��ʾ�����ӣ�ͼ�е����е㣬�߶���ͬһƽ���ڣ�������ͼ���ҳ��������ƶ���ȫ�ȵ������Σ���˵���������Ƶ����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
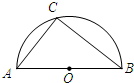 ��ͼ����C���Ե�OΪԲ�ģ�ABΪֱ���İ�Բ�ϵĶ��㣨��C�����A��B�غϣ���AB=4������AC�ij�Ϊx����ABC�����Ϊy��������ͼ���У��ܱ�ʾy��x�ĺ�����ϵ��ͼ������ǣ�������
��ͼ����C���Ե�OΪԲ�ģ�ABΪֱ���İ�Բ�ϵĶ��㣨��C�����A��B�غϣ���AB=4������AC�ij�Ϊx����ABC�����Ϊy��������ͼ���У��ܱ�ʾy��x�ĺ�����ϵ��ͼ������ǣ�������| A�� | 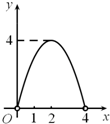 | B�� | 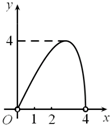 | C�� | 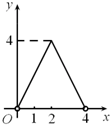 | D�� | 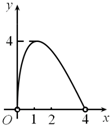 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
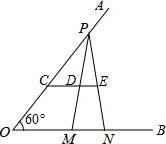 ��ͼ����֪��AOB=60�㣬��P�ڱ�OA�ϣ�OP=10����M��N�ڱ�OB�ϣ�PM=PN����CΪ�߶�OP������һ�㣬CD��ON��PM��PN�ֱ�ΪD��E����MN=3����$\frac{CD}{DE}$��ֵΪ$\frac{7}{6}$��
��ͼ����֪��AOB=60�㣬��P�ڱ�OA�ϣ�OP=10����M��N�ڱ�OB�ϣ�PM=PN����CΪ�߶�OP������һ�㣬CD��ON��PM��PN�ֱ�ΪD��E����MN=3����$\frac{CD}{DE}$��ֵΪ$\frac{7}{6}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com