
【题目】如图,在下面的方格纸中,找出互相平行的线段,并用符号表示出来:__________,__________.
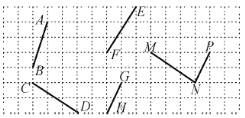
【答案】CD∥MN;GH∥PN
【解析】
AB,竖直方向的长度为3个单位,水平方向的长度为1个单位,比值为:3:1,
CD,竖直方向的长度为2个单位,水平方向的长度为3个单位,比值为:2:3,
EF,竖直方向的长度为3个单位,水平方向的长度为2个单位,比值为:3:2,
GH,竖直方向的长度为2个单位,水平方向的长度为1个单位,比值为:2:1,
MN,竖直方向的长度为2个单位,水平方向的长度为3个单位,比值为:2:3,
PN,竖直方向的长度为2个单位,水平方向的长度为1个单位,比值为:2:1,
结合图形线段的倾斜方向相同,比值相同的线段是CD与MN,GH与PN,
∴互相平行的线段是CD∥MN,GH∥PN,故答案为:CD∥MN,GH∥PN.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
【题目】11世纪的一位阿拉伯数学家曾提出一个“鸟儿捉鱼”问题:小溪边长着两棵棕榈树,恰好隔岸相望一棵棕榈树高是30肘尺(肘尺是古代的长度单位),另外一棵高20肘尺;两棵棕榈树的树干间的距离是50肘尺.每棵树的树顶上都停着一只鸟.忽然,两只鸟同时看见棕榈树间的水面上游出一条鱼,它们立刻以相同的速度飞去抓鱼,并且同时到达目标.问:这条鱼出现的地方离比较高的棕榈树的树根有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠ABC=60°,AB=2,点P是这个菱形内部或边上的一点,若以点P、B、C为顶点的三角形是等腰三角形,则P、D(P、D两点不重合)两点间的最短距离为 . 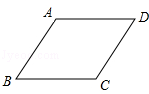
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个反比例函数y1= ![]() (其中k1>0)和y2=
(其中k1>0)和y2= ![]() 在第一象限内的图象依次是C1和C2 , 点P在C1上.矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF⊥x轴于F点,且图中四边形BOAP的面积为6,则EF:AC为( )
在第一象限内的图象依次是C1和C2 , 点P在C1上.矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF⊥x轴于F点,且图中四边形BOAP的面积为6,则EF:AC为( ) 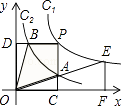
A.![]() ﹕1
﹕1
B.2﹕ ![]()
C.2﹕1
D.29﹕14
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,在探究筝形的性质时,得到如下结论:①△ABD≌△CBD;②AC⊥BD;③四边形ABCD的面积= ![]() ACBD,其中正确的结论有( )
ACBD,其中正确的结论有( ) 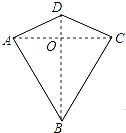
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠1=∠2,G为AD边上的中点,延长BG交AC于点E,且满足BE⊥AC;F为AB上一点,CF⊥AD于点H.下列判断:①线段AG是△ABE的角平分线;②BE是△ABD边AD上的中线;③线段AE是△ABG的边BG上的高;④∠1+∠FBC+∠FCB=90°.其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,根据图形解答下列问题:
(1)写出能用一个字母表示的角;
(2)写出以点B为顶点的角;
(3)写出以BC为边的角;
(4)图中共有几个角(小于平角的角)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市在一次市政施工中,有两段长度相等的人行道铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设人行道的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题: 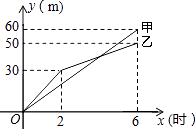
(1)求乙队在2≤x≤6的时间段内,y与x的函数关系式;
(2)若甲队施工速度不变,乙队在施工6小时后,施工速度增加到12米/时,结果两队同时完成了任务.求甲队从开始施工到完成,所铺设的人行道共是多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com