
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌAB=4.41cmЃЌBC=8.83cmЃЌPЪЧBCЩЯвЛЖЏЕуЃЌСЌНгAPЃЌЩшPЃЌCСНЕуМфЕФОрРыЮЊxcmЃЌPЃЌAСНЕуМфЕФОрРыЮЊycmЃЎЃЈЕБЕуPгыЕуCжиКЯЪБЃЌxЕФжЕЮЊ0ЃЉаЁЖЋИљОнбЇЯАКЏЪ§ЕФОбщЃЌЖдКЏЪ§yЫцздБфСПxЕФБфЛЏЖјБфЛЏЕФЙцТЩНјааСЫЬНОПЃЎЯТУцЪЧаЁЖЋЕФЬНОПЙ§ГЬЃЌЧыВЙГфЭъећЃК
ЃЈ1ЃЉЭЈЙ§ШЁЕуЁЂЛЭМЁЂВтСПЃЌЕУЕНСЫxгыyЕФМИзщжЕЃЌШчБэЃК
x/cm | 0 | 0.43 | 1.00 | 1.50 | 1.85 | 2.50 | 3.60 | 4.00 | 4.30 | 5.00 | 5.50 | 6.00 | 6.62 | 7.50 | 8.00 | 8.83 |
y/cm | 7.65 | 7.28 | 6.80 | 6.39 | 6.11 | 5.62 | 4.87 | 4.47 | 4.15 | 3.99 | 3.87 | 3.82 | 3.92 | 4.06 | 4.41 |
ЃЈЫЕУїЃКВЙШЋБэИёЪБЯрЙиЪ§жЕБЃСєвЛЮЛаЁЪ§ЃЉ
ЃЈ2ЃЉНЈСЂЦНУцжБНЧзјБъЯЕЃЌУшГівдВЙШЋКѓЕФБэжаИїЖдЖдгІжЕЮЊзјБъЕФЕуЃЌЛГіИУКЏЪ§ЕФЭМЯѓЃЛ
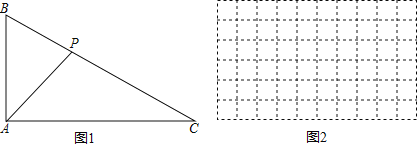
ЃЈ3ЃЉНсКЯЛГіЕФКЏЪ§ЭМЯѓЃЌНтОіЮЪЬтЃКЕБPA=PCЪБЃЌPCЕФГЄЖШдМЮЊ cmЃЎЃЈНсЙћБЃСєвЛЮЛаЁЪ§ЃЉ
 гРЧЌНЬг§КЎМйзївЕПьРжМйЦкбгБпШЫУёГіАцЩчЯЕСаД№АИ
гРЧЌНЬг§КЎМйзївЕПьРжМйЦкбгБпШЫУёГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвде§ЗНаЮABCDвЛБпABЮЊБпзїЕШБпШ§НЧаЮABEЃЌдђЁЯCEDЃН_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЕу
жаЃЌЕу![]() зјБъЮЊ
зјБъЮЊ![]() ЃЌвддЕу
ЃЌвддЕу![]() ЮЊЖЅЕуЕФЫФБпаЮ
ЮЊЖЅЕуЕФЫФБпаЮ![]() ЪЧЦНааЫФБпаЮЃЌНЋБп
ЪЧЦНааЫФБпаЮЃЌНЋБп![]() би
би![]() жсЗелЕУЕНЯпЖЮ
жсЗелЕУЕНЯпЖЮ![]() ЃЌСЌНс
ЃЌСЌНс![]() НЛЯпЖЮ
НЛЯпЖЮ![]() гкЕу
гкЕу![]() .
.
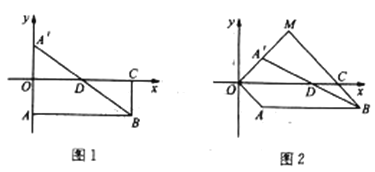
ЃЈ1ЃЉШчЭМ1ЃЌЕБЕу![]() дк
дк![]() жсЩЯЃЌЧвЦфзјБъЮЊ
жсЩЯЃЌЧвЦфзјБъЮЊ![]() .
.
ЂйЧѓ![]() ЫљдкжБЯпЕФКЏЪ§БэДяЪНЃЛ
ЫљдкжБЯпЕФКЏЪ§БэДяЪНЃЛ
ЂкЧѓжЄЃКЕу![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЕФжаЕуЃЛ
ЕФжаЕуЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ![]() ЕФбгГЄЯпЯрНЛгкЕу
ЕФбгГЄЯпЯрНЛгкЕу![]() ЃЌЪдЧѓ
ЃЌЪдЧѓ![]() ЕФжЕ.ЃЈжБНгаДГіД№АИЃЌВЛБиЫЕУїРэгЩЃЉ
ЕФжЕ.ЃЈжБНгаДГіД№АИЃЌВЛБиЫЕУїРэгЩЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌPЪЧЯпЖЮABЩЯШЮвЛЕуЃЌABЃН12 cmЃЌCЁЂDСНЕуЗжБ№ДгPЁЂBЭЌЪБЯђAЕудЫЖЏЃЌЧвCЕуЕФдЫЖЏЫйЖШЮЊ2 cm/sЃЌDЕуЕФдЫЖЏЫйЖШЮЊ3 cm/sЃЌдЫЖЏЕФЪБМфЮЊt s.
![]()
(1)ШєAPЃН8 cm.
ЂйдЫЖЏ1 sКѓЃЌЧѓCDЕФГЄЃЛ
ЂкЕБDдкЯпЖЮPBдЫЖЏЩЯЪБЃЌЪдЫЕУїACЃН2CDЃЛ
(2)ШчЙћtЃН2 sЪБЃЌCDЃН1 cmЃЌЪдЬНЫїAPЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫДйНјбЇЩњЬхг§ЖЭСЖЃЌФГаЃАЫФъМЖНјааСЫЬхг§ВтЪдЃЌЮЊСЫНтХЎЩњЬхг§ВтЪдЧщПіЃЌДгжаГщШЁСЫШєИЩУћХЎЩњЕФЬхг§ВтЪдГЩМЈ.
a.Ьхг§ЮЏдБаЁРюдкећРэЦЕЪ§ЗжВМБэЪБЃЌВЛаЁаФЮлШОСЫЭГМЦБэЃК
ЗжзщЃЈЗжЃЉ | ЦЕЪ§ | ЦЕЪ§ |
21ЃМxЁм22 | 8 | 0.200 |
22ЃМxЁм23 | 4 | n |
23ЃМxЁм24 | 7 | 0.175 |
24ЃМxЁм25 | 3 | 0.075 |
25ЃМxЁм26 | 2 | 0.050 |
26ЃМxЁм27 | 8 | 0.200 |
27ЃМxЁм28 | m | 0.150 |
28ЃМxЁм29 | 2 | 0.050 |
КЯМЦ |
|
bЃЎИљОнЦЕЪ§ЗжВМБэЃЌЛцжЦШчЯТЦЕЪ§ЗжВМжБЗНЭМЃК
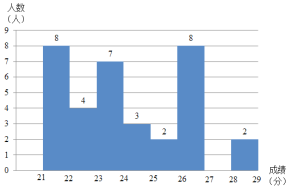
cЃЎдкДЫДЮВтЪджаЃЌЙВВтЪдСЫ800УзЃЌРКЧђЃЌбіЮдЦ№зјЃЌГЩМЈЭГМЦШчЯТЃК
ЯюФП | ЦНОљЗж | жаЮЛЪ§ | жкЪ§ |
800Уз | 8.27 | 8.5 | 8.5 |
біЮдЦ№зј | 7.61 | 8 | 7.5 |
РКЧђ | 8.69 | 9 | 8 |
ИљОнвдЩЯаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉаДГіБэжаmЃЌnЕФжЕЃЛ
ЃЈ2ЃЉВЙШЋжБЗНЭМЃЛ
ЃЈ3ЃЉЧыНсКЯCжаЭГМЦЭМБэЃЌИјИУаЃХЎЩњЬхг§бЕСЗЬсЙЉНЈвщЃЈжСЩйДгСНИіВЛЭЌЕФНЧЖШЗжЮіЃЉ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСЯТУцВФСЯЃК
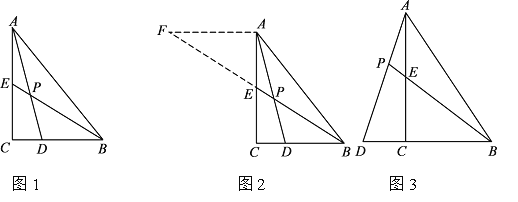
аЁъЛгіЕНетбљвЛИіЮЪЬтЃКШчЭМ1ЃЌдкЁїABCжаЃЌЁЯACB=90ЁуЃЌBEЪЧACБпЩЯЕФжаЯпЃЌЕуDдкBCБпЩЯЃЌCDЃКBD=1ЃК2ЃЌADгыBEЯрНЛгкЕуPЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
аЁъЛЗЂЯжЃЌЙ§ЕуAзїAFЁЮBCЃЌНЛBEЕФбгГЄЯпгкЕуFЃЌЭЈЙ§ЙЙдьЁїAEFЃЌОЙ§ЭЦРэКЭМЦЫуФмЙЛЪЙЮЪЬтЕУЕННтОіЃЈШчЭМ2ЃЉЃЎЧыЛиД№ЃК![]() ЕФжЕЮЊЁЁЃЎ
ЕФжЕЮЊЁЁЃЎ
ВЮПМаЁъЛЫМПМЮЪЬтЕФЗНЗЈЃЌНтОіЮЪЬтЃК
ШчЭМ 3ЃЌдкЁїABCжаЃЌЁЯACB=90ЁуЃЌЕуDдкBCЕФбгГЄЯпЩЯЃЌADгыACБпЩЯЕФжаЯпBEЕФбгГЄЯпНЛгкЕуPЃЌDCЃКBCЃКAC=1ЃК2ЃК3 ЃЎ
ЃЈ1ЃЉЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉШєCD=2ЃЌдђBP=__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдке§ЗНаЮЭјИёжаЃЌНЈСЂШчЭМЫљЪОЕФЦНУцжБНЧзјБъЯЕxOyЃЌЁїABCЕФШ§ИіЖЅЕуЖМдкИёЕуЩЯЃЌЕуAЕФзјБъЃЈ4ЃЌ4ЃЉЃЌЧыНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЛГіЁїABCЙигкyжсЖдГЦЕФЁїA1B1C1ЃЌВЂаДГіЕуA1ЁЂB1ЁЂC1ЕФзјБъЃЛ
ЃЈ2ЃЉНЋЁїABCШЦЕуCФцЪБеыа§зЊ90ЁуЃЌЛГіа§зЊКѓЕФЁїA2B2C2ЃЌВЂЧѓГіЕуAЕНA2ЕФТЗОЖГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌCЮЊЯпЖЮABЕФжаЕуЃЌЕуDдкЯпЖЮCBЩЯЃЎ
![]()
ЃЈ1ЃЉЭМжаЙВга ЬѕЯпЖЮЃЎ
ЃЈ2ЃЉЭМжаAD=AC+CDЃЌBC=ABЉACЃЌРрЫЦЕиЃЌЧыФудйаДГіСНИігаЙиЯпЖЮЕФКЭгыВюЕФЙиЯЕЪНЃК
Ђй ЃЛЂк .
ЃЈ3ЃЉШєAB=8ЃЌDB=1.5ЃЌЧѓЯпЖЮCDЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЯпЖЮABКЭCDЕФЙЋЙВВПЗжBD=![]() AB=
AB= ![]() CDЃЌЯпЖЮABЁЂCDЕФжаЕуEЃЌFжЎМфОрРыЪЧ10cmЃЌЧѓABЃЌCDЕФГЄЃЎ
CDЃЌЯпЖЮABЁЂCDЕФжаЕуEЃЌFжЎМфОрРыЪЧ10cmЃЌЧѓABЃЌCDЕФГЄЃЎ
![]()
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com