
 ȥ��2�·���Ѯ��ij˫�����Ի���ѧ��֯��ְ���Լ�����������ʯ��ʱ���м�����ѧ��ʦ������һ�����ºӵĽ��ڴ���һ��������״����Ȼ������δ��ˮʱ���ˮ���AB��10�ף�����ˮˮ������4���ˮ���CDΪ6�ף�
ȥ��2�·���Ѯ��ij˫�����Ի���ѧ��֯��ְ���Լ�����������ʯ��ʱ���м�����ѧ��ʦ������һ�����ºӵĽ��ڴ���һ��������״����Ȼ������δ��ˮʱ���ˮ���AB��10�ף�����ˮˮ������4���ˮ���CDΪ6�ף����� ��1����AB���е�Ϊ����ԭ�㽨������ϵ����B��5��0��D��3��4����y=ax2+c��ͼ���ϣ������������ʽ���������ˮǰ����ˮ�浽�����ĸ߶ȣ�
��2����x=0.8���뺯������ʽ���y��ֵ��6�Ƚϼ��������жϣ�
��� �⣺��1����AB���е�Ϊ����ԭ�㽨������ϵ���躯������ʽΪy=ax2+c��
��B��5��0��D��3��4����y=ax2+c��ͼ���ϣ�
��$\left\{\begin{array}{l}{25a+c=0}\\{9a+c=4}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{a=-\frac{1}{4}}\\{c=\frac{25}{4}}\end{array}\right.$��
��y=-$\frac{1}{4}$x2+$\frac{25}{4}$��
����ˮǰ������ˮ�浽�����ĸ߶�Ϊ$\frac{25}{4}$�ף���ˮ����ˮ�浽�����ĸ߶�Ϊ$\frac{25}{4}$-4=$\frac{9}{4}$�ף�
��2����x=0.8���뺯������ʽ��
y=-$\frac{1}{4}$��$\frac{16}{25}$+$\frac{25}{4}$=6.09��6��
����ֻ�����ο͵��δ�������ͨ��������
���� ������Ҫ�����˶��κ�����Ӧ�ã��ڽ���ʱҪ�������⽨������ϵ���ٸ��������ĵ��������ʽ�DZ���Ĺؼ���


 ������ҵ��ͬ����ϰ��ϵ�д�
������ҵ��ͬ����ϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
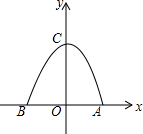 ij��ũ�һ�������Ϊ�����ߵĴ��������ͼ��ʾ��ֱ������ϵ�������ߵı���ʽy=-$\frac{1}{2}{x}^{2}$+2��
ij��ũ�һ�������Ϊ�����ߵĴ��������ͼ��ʾ��ֱ������ϵ�������ߵı���ʽy=-$\frac{1}{2}{x}^{2}$+2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
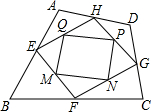 ��ͼ�����ı���ABCD�У����ν�����ߵ��е�E��F��G��H�����������õ����ı���EFGH��ƽ���ı��Σ������ν��ı���EFGH���ߵ��е�M��N��P��Q�����������õ����ı���MNPQ��
��ͼ�����ı���ABCD�У����ν�����ߵ��е�E��F��G��H�����������õ����ı���EFGH��ƽ���ı��Σ������ν��ı���EFGH���ߵ��е�M��N��P��Q�����������õ����ı���MNPQ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{1}{4}$ | D�� | $\frac{1}{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com