Question

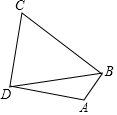
2．已知：在四边形ABCD中，∠ABC=90°，∠C=60，AB=$\frac{\sqrt{3}}{2}$，BC=1+$\sqrt{3}$，CD=2
（1）求tan∠ABD的值； 
（2）求AD的长．

Answer 1

分析 （1）作DE⊥BC，由∠C=60°、CD=2知CE=1，DE=$\sqrt{3}$，结合BC的长知BE=DE，即∠EDB=∠EBD=45°，根据∠ABC=90°得∠ABD=45°，从而得出答案；
（2）作AF⊥BD，先求出BF=AF=$\frac{\sqrt{6}}{4}$，根据BE=DE=$\sqrt{3}$求得BD=$\sqrt{6}$、DF=$\frac{3\sqrt{6}}{4}$，最后根据勾股定理可得答案．

解答 解：（1）如图，作DE⊥BC于点E．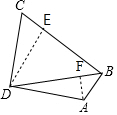

∵在Rt△CDE 中，∠C=60°，CD=2，
∴CE=1，DE=$\sqrt{3}$，
∵BC=1+$\sqrt{3}$，
∴BE=$\sqrt{3}$．
∴BE=DE
∵∠DEB=90°，
∴∠EDB=∠EBD=45°．
∵AB⊥BC，∠ABC=90°，
∴∠ABD=∠ABC-∠EBD=45°．
∴tan∠ABD=1．

（2）如图，作AF⊥BD于点F．
在Rt△ABF 中，∠ABF=45°，AB=$\frac{\sqrt{3}}{2}$，
∴BF=AF=$\frac{\sqrt{6}}{4}$．
∵在Rt△BDE 中，BE=DE=$\sqrt{3}$，
∴BD=$\sqrt{6}$．
∴DF=$\frac{3\sqrt{6}}{4}$．
∴在Rt△AFD 中，由勾股定理得：AD=$\frac{\sqrt{15}}{2}$．

点评 本题主要考查解直角三角形，掌握解直角三角形要用到的关系 ①锐角直角的关系：∠A+∠B=90°； ②三边之间的关系：a²+b²=c²； ③边角之间的关系是解题的关键．