

【小题1】如图①,一张三角形ABC纸片,点D、E分别是△ABC边上两点.
研究(1):如果沿直线DE折叠,使A点落在CE上,则∠BDA′与∠A的数量关系是__ ▲_________
∠BDA′=2∠A
∠BDA′+∠CEA′=2∠A
【小题2】如果折成图②的形状,猜想∠BDA′、∠CEA和∠A的数量关系是__ ▲_________
【小题3】如果折成图③的形状,猜想∠BDA′、∠CEA′和∠A的数量关系,并说明理由.
猜想:▲________
【小题4】将问题1推广,如图,将四边形ABCD纸片沿EF折叠,使点A、B落在四边形EFCD的内部时,∠1+∠2与∠A、∠B之间的数量关系是_ ▲________
【小题1】∠BDA′=2∠A
【小题2】∠BDA′+∠CEA′=2∠A
【小题3】∠BDA-∠CEA=2∠A
【小题4】∠1+∠2=2(∠A+∠B)-360°
解析解:①根据折叠的性质可知∠DA′E=∠A,∠DA′E+∠A=∠BDA′,故∠BDA′=2∠A;
②由图形折叠的性质可知,∠CEA′=180°-2∠DEA′…①,∠BDA′=180°-2∠A′DE…②,
①+②得,∠BDA′+∠CEA′=360°-2(∠DEA′+∠A′DE
即∠BDA′+∠CEA′=360°-2(180°-∠A),
故∠BDA′+∠CEA′=2∠A;
③∠BDA′-∠CEA′=2∠A.
证明如下:
连接AA′构造等腰三角形,
∠BDA′=2∠DA'A,∠CEA'=2∠EA'A,
得∠BDA'-∠CEA'=2∠A,
④由图形折叠的性质可知∠1=180°-2∠AEF,∠2=180°-2∠BFE,
两式相加得,∠1+∠2=360°-2(∠AEF+∠BFE)
即∠1+∠2=360°-2(360°-∠A-∠B),
即∠1+∠2=2(∠A+∠B)-360°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 )=1.
)=1. 个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移
个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移 个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为
个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为 .
.
查看答案和解析>>
科目:初中数学 来源:2012届江西省新余市中考模拟考试数学试卷(带解析) 题型:解答题
已知:如图(1),△OAB是边长为2的等边三角形,0A在x轴上,点B在第一象限内;△OCA是一个等腰三角形,OC=AC,顶点C在第四象限,∠C=120°.现有两动点P、Q分别从A、O两点同时出发,点Q以每秒1个单位的速度沿OC向点C运动,点P以每秒3个单位的速度沿A→O→B运动,当其中一个点到达终点时,另一个点也随即停止.
【小题1】求在运动过程中形成的△OPQ的面积S与运动的时间t之间的函数关系,并写出自变量t的取值范围;
【小题2】在OA上(点O、A除外)存在点D,使得△OCD为等腰三角形,请直接写出所有符合条件的点D的坐标;
【小题3】如图(2),现有∠MCN=60°,其两边分别与OB、AB交于点M、N,连接MN.将∠MCN绕着C点旋转(0°<旋转角<60°),使得M、N始终在边OB和边AB上.试判断在这一过程中,△BMN的周长是否发生变化?若没有变化,请求出其周长;若发生变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2012年人教新课标版中考综合模拟数学卷(11) 题型:解答题
类比学习:一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位.用实数加法表示为 3+(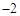 )=1.
)=1.
若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移 个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移
个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移 个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为
个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为 .
.
解决问题:
【小题1】计算:{3,1}+{1,2};{1,2}+{3,1}.
【小题2】①动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量”{1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量”{3,1}平移,最后的位置还是点B吗? 在图1中画出四边形OABC.
②证明四边形OABC是平行四边形.
【小题3】如图2,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,2),最后回到出发点O. 请用“平移量”加法算式表示它的航行过程.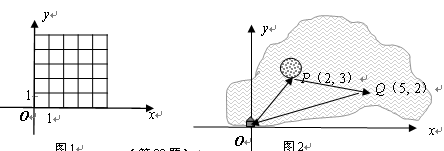
查看答案和解析>>
科目:初中数学 来源:2011-2012学年北京市101中学下学期七年级期中考试数学试卷(带解析) 题型:解答题
类比学习:一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位。用有理数加法表示为3+(-2)=1。 若坐标平面上的点做如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移 个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移
个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移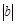 个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为
个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为 。
。
解决问题:
【小题1】计算:{3,1}+{1,-2};
【小题2】动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量”
{1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量”
{3,1}平移,最后的位置还是点B吗? 在图1中画出四边形OABC。
【小题3】如图2,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O. 请用“平移量”加法算式表示它的航行过程。
查看答案和解析>>
科目:初中数学 来源:2012年江苏省南京市溧水县中考二模数学试卷(带解析) 题型:解答题
如图①,将一张直角三角形纸片ABC折叠,使点A与点C重合,这时DE为折痕,△CBE为等腰三角形,再继续将纸片沿△CBE的对称轴EF折叠,这时得到了两个完全重合的矩形(其中一个是原三角形的内接矩形,另一个是拼合成的无缝隙、无重叠的矩形),我们称这样的两个矩形为“叠加矩形”.请完成下列问题: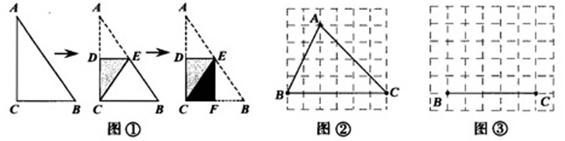
【小题1】如图②,正方形网格中的△ABC能折叠成“叠加矩形”吗?如能,请在图②中画出折痕;
【小题2】如图③,在正方形网格中,以给定的BC为一边,画出一个斜△ABC,使其顶点A在格点上,且△ABC折成的“叠加矩形”为正方形;
【小题3】如果一个三角形所折成的“叠加矩形” 为正方形,那么它必须满足的条件是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com