
如图所示,已知 ,
, 为反比例函数
为反比例函数 图像上的两点,动点
图像上的两点,动点 在
在 正半轴上运动,当线段
正半轴上运动,当线段 与线段
与线段 之差达到最大时,点
之差达到最大时,点 的坐标是( )
的坐标是( )
A. | B. | C. | D. |
D
解析试题分析:先求出A、B的坐标,再根据待定系数法求出直线AB的解析式,根据三角形的三边关系定理得出在△ABP中,  ,延长AB交x轴于P′,当P在P′点时,
,延长AB交x轴于P′,当P在P′点时, ,此时线段AP与线段BP之差达到最大,求出直线AB于x轴的交点坐标即可.
,此时线段AP与线段BP之差达到最大,求出直线AB于x轴的交点坐标即可.
由 ,
, 为反比例函数
为反比例函数 图像上的两点,
图像上的两点,
可得A( ,2),B(2,
,2),B(2, ),
),
∵在△ABP中, ,
,
∴延长AB交x轴于P′,当P在P′点时, ,
,
即此时线段AP与线段BP之差达到最大,
设直线AB的解析式是y=kx+b,
∵图象过点A( ,2),B(2,
,2),B(2, ),
), ,解得
,解得 ,
,
∴直线AB的解析式是 ,
,
当 时,
时, ,
,
即P ,
,
故选D.
考点:本题考查的是三角形的三边关系,用待定系数法求一次函数的解析式
点评:解答本题的关键是熟练掌握三角形的三边关系:三角形的任两边之和大于第三边;本题中确定P点的位置是突破口.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 在八年级上册我们已经知道三角形的中位线具有如下性质:
在八年级上册我们已经知道三角形的中位线具有如下性质:| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:同步轻松练习 九年级 数学 上 题型:047
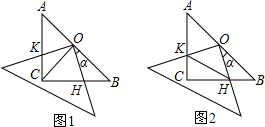
如图所示,已知正方形ABCD和正方形EFFG有一个公共点A,点G,E不在线段AD,AB上.

(1)如图,连接DF,BF,若将正方形AEFG绕点A按顺时针方向旋转,判断命题:“在旋转的过程中,线段DF与线段BF的长始终相等”是否正确,若正确请证明;若不正确,请举反例说明.
(2)若将正方形AEFG绕点A按顺时针方向旋转,连接DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等,并以图②为例说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
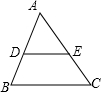 在八年级上册我们已经知道三角形的中位线具有如下性质:
在八年级上册我们已经知道三角形的中位线具有如下性质: BC;④DE∥BC.
BC;④DE∥BC.查看答案和解析>>
科目:初中数学 来源:福建省中考真题 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com