
【题目】如图,等腰△ABC中,AB=AC,∠ACB=72°,

(1)若BD⊥AC于D,求∠ABD的度数;
(2)若CE平分∠ACB,求证:AE=BC.
【答案】(1)54°;(2)见解析
【解析】
(1)根据等腰三角形的性质得出∠ABC=∠ACB=72°,然后计算出∠DBC,即可计算∠ABD的度数;
(2)根据角平分线的性质计算有关度数,分别证明AE=EC 和BC=CE即可.
(1)∵等腰△ABC中,AB=AC,∠ACB=72°,
∴∠ABC=∠ACB=72°,
∵BD⊥AC于D,
∴∠DBC=90°-72°=18°,
∴∠ABD=72°-18°=54°;
(2)∵等腰△ABC中,AB=AC,∠ACB=72°,
∴∠ABC=∠ACB=72°,∠A=36°
∵CE平分∠ACB,
∴∠ACE=∠ECB=36°,
∴∠A=∠ACE,
∴AE=EC,∠BEC=72°
∵∠ABC=72°,
∴∠ABC=∠BEC,
∴BC=CE,
∴AE=BC.


科目:初中数学 来源: 题型:
【题目】如图,甲、乙两船从港口A同时出发,甲船以30海里/时的速度向北偏东35°的方向航行,乙船以40海里/时的速度向另一方向航行,2小时后,甲船到达C岛,乙船到达B岛,若C,B两岛相距100海里,则乙船航行的方向是南偏东多少度?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与直线CD相交于点O,EO⊥AB,OF平分∠AOC,
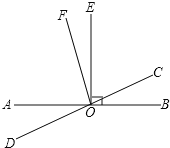
(1)请写出∠EOC的余角 ;
(2)若∠BOC=40°,求∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[知识背景]:
数轴上,点A,B表示的数为a,b,则A,B两点的距离AB=|a﹣b|,A、B的中点P表示的数为![]() .
.
[知识运用]:
已知式子(a+4)x3+2x2﹣x+3是关于x的二次三项式,且二次项系数为b,且a,b在数轴上对应的点分别为A,B(如图1),解答下列问题:
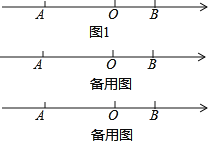
(1)a= ,b= ,AB= ;
(2)若点A以每秒2个单位的长度沿数轴向右运动,t秒后到达原点O,求t的值;
(3)若点A,B都以每秒2个单位长度的速度沿数轴向右运动到达点M和点N,而O点不动,经过t秒后,M,O,N三点中,其中一点是另外两点的中点,求此时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明星期天从家里出发骑车去舅舅家做客,当他骑了一段路时,想起要买个礼物送给表弟,于是又折回到刚经过的一家商店,买好礼物后又继续骑车去舅舅家,以下是他本次去舅舅家所用的时间与路程的关系式示意图,根据图中提供的信息回答下列问题:
(1)小明家到舅舅家的路程是______米,小明在商店停留了______分钟;
(2)在整个去舅舅家的途中哪个时间段小明骑车速度最快,最快的速度是多少米/
分?
(3)本次去舅舅家的行程中,小明一共行驶了多少米?一共用了多少分钟?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两支“徒步队”到野外沿相同路线徒步,徒步的路程为24千米.甲队步行速度为4千米/时,乙队步行速度为6千米/时.甲队出发1小时后,乙队才出发,同时乙队派一名联络员跑步在两队之间来回进行一次联络(不停顿),他跑步的速度为10千米/时.
(1)乙队追上甲队需要多长时间?
(2)联络员从出发到与甲队联系上后返回乙队时,他跑步的总路程是多少?
(3)从甲队出发开始到乙队完成徒步路程时止,何时两队间间隔的路程为1千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生会调查了八年级部分学生对“垃圾分类”的了解程度(1)在确定调查方式时,学生会设计了以下三种方案,其中最具有代表性
的方案是________;
方案一:调查八年级部分男生;
方案二:调查八年级部分女生;
方案三:到八年级每个班去随机调查一定数量的学生.
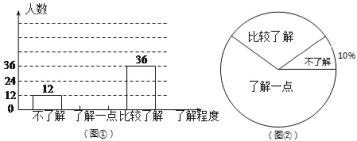
(2)学生会采用最具有代表性的方案进行调查后,将收集到的数据绘制成如下两幅不完整的统计图,如图①、图②.请你根据图中信息,回答下列问题:
①本次调查学生人数共有_______名;
②补全图①中的条形统计图,图②中了解一点的圆心角度数为_______;
③根据本次调查,估计该校八年级500名学生中,比较了解“垃圾分类”的学生大约有_______名.
查看答案和解析>>
科目:初中数学 来源: 题型:
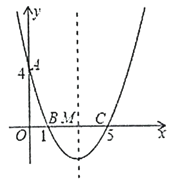
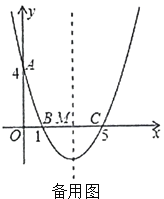
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于
轴交于![]() 两点,其对称轴与
两点,其对称轴与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线的解析式和对称轴;
(2)在抛物线的对称轴上是否存在一点![]() ,使
,使![]() 的周长最小?若存在,请求出点
的周长最小?若存在,请求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)连接![]() ,在直线
,在直线![]() 的下方的抛物线上,是否存在一点
的下方的抛物线上,是否存在一点![]() ,使
,使![]() 的面积最大?若存在,请求出点
的面积最大?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com