
【题目】如图,过抛物线y= ![]() x2﹣2x上一点A作x轴的平行线,交抛物线于另一点B,交y轴于点C,已知点A的横坐标为﹣2.
x2﹣2x上一点A作x轴的平行线,交抛物线于另一点B,交y轴于点C,已知点A的横坐标为﹣2.
(1)求抛物线的对称轴和点B的坐标;
(2)在AB上任取一点P,连结OP,作点C关于直线OP的对称点D;
①连结BD,求BD的最小值;
②当点D落在抛物线的对称轴上,且在x轴上方时,求直线PD的函数表达式.
【答案】
(1)
解:由题意A(﹣2,5),对称轴x=﹣ ![]() =4,
=4,
∵A、B关于对称轴对称,
∴B(10,5).
(2)
解:①如图1中,
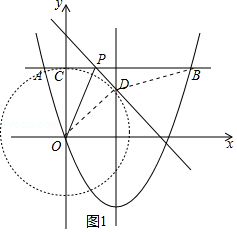
由题意点D在以O为圆心OC为半径的圆上,
∴当O、D、B共线时,BD的最小值=OB﹣OD= ![]() ﹣5=5
﹣5=5 ![]() ﹣5.
﹣5.
②如图中,
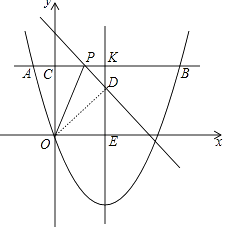
当点D在对称轴上时,在Rt△ODE中,OD=OC=5,OE=4,
∴DE= ![]() =
= ![]() =3,
=3,
∴点D的坐标为(4,3).
设PC=PD=x,在Rt△PDK中,x2=(4﹣x)2+22,
∴x= ![]() ,
,
∴P( ![]() ,5),
,5),
∴直线PD的解析式为y=﹣ ![]() x+
x+ ![]() .
.
【解析】(1)思想确定点A的坐标,利用对称轴公式求出对称轴,再根据对称性可得点B坐标;(2)①由题意点D在以O为圆心OC为半径的圆上,推出当O、D、B共线时,BD的最小值=OB﹣OD;②当点D在对称轴上时,在Rt△OD=OC=5,OE=4,可得DE= ![]() =
= ![]() =3,求出P、D的坐标即可解决问题;
=3,求出P、D的坐标即可解决问题;
【考点精析】通过灵活运用抛物线与坐标轴的交点,掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.即可以解答此题.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:
【题目】综合题。
(1)计算:(π﹣ ![]() )0+
)0+ ![]() +(﹣1)2013﹣
+(﹣1)2013﹣ ![]() tan60°;
tan60°;
(2)先化简,再求值:(a+3)2+a(4﹣a),其中a为(1)中计算的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用若干个大小相同,棱长为1的小正方体搭成一个几何体模型,其三视图如图所示,则搭成这个几何体模型所用的小正方体的个数是( )

A. 4 B. 5 C. 6 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A点的初始位置位于数轴上表示1的点,现对A点做如下移动:第1次向左移动3个单位长度至B点,第2次从B点向右移动6个单位长度至C点,第3次从C点向左移动9个单位长度至D点,第4次从D点向右移动12个单位长度至E点,…,依此类推.这样第_____次移动到的点到原点的距离为2018.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为创建大数据应用示范城市,我市某机构针对市民最关心的四类生活信息进行了民意调查(被调查者每人限选一项),下面是部分四类生活信息关注度统计图表,请根据图中提供的信息解答下列问题:
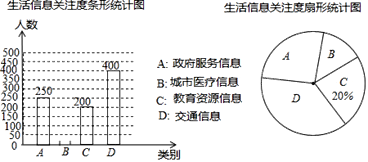
(1)本次参与调查的人数有______ 人;
(2)关注城市医疗信息的有______ 人,并补全条形统计图;
(3)扇形统计图中,D部分的圆心角是______度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区准备新建50个停车位,用以解决小区停车难的问题.已知新建1个地上停车位和1个地下停车位共需0.6万元;新建3个地上停车位和2个地下停车位共需1.3万元.
(1)该小区新建1个地上停车位和1个地下停车位各需多少万元?
(2)该小区的物业部门预计投资金额超过12万元而不超过13万元,那么共有几种建造停车位的方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一元一次方程的解也是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.
例如:方程![]() 的解为
的解为![]() ,不等式组
,不等式组![]() 的解集为
的解集为![]() ,因为
,因为![]() ,所以,称方程
,所以,称方程![]() 为不等式组
为不等式组![]() 的关联方程.
的关联方程.
(1)在方程①![]() ,②
,②![]() ,③
,③![]() 中,不等式组
中,不等式组![]() 的关联方程是 ;(填序号)
的关联方程是 ;(填序号)
(2)若不等式组 的一个关联方程的根是整数,则这个关联方程可以是 ;(写出一个即可)
的一个关联方程的根是整数,则这个关联方程可以是 ;(写出一个即可)
(3)若方程![]() ,
,![]() 都是关于
都是关于![]() 的不等式组
的不等式组![]() 的关联方程,求
的关联方程,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,EF与AB、CD分别相交于点E、F,EP⊥EF,与∠EFD的平分线FP相交于点P,且∠BEP=50°,则∠EPF=( )度. 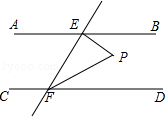
A.70
B.65
C.60
D.55
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com