练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

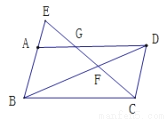
    已知平行四边形ABCD，E是BA延长线上一点，CE与AD、BD交于G、F．求证：CF2=GF•EF．

    证明见解析 【解析】试题分析：根据平行四边形的性质，得到平行关系，然后根据平行线分线段成比例可证明. 试题解析：∵四边形ABCD是平行四边形， ∴AD∥BC，AB∥CD， ∴GF:CF=DF:BF，CF:EF=DF:BF， ∴GF:CF=CF:EF， 即CF2=GF•EF．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年九年级数学人教版上册：第23章 旋转 单元测试卷 题型：填空题

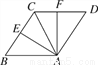
    如图，将等边△ABC绕顶点A按顺时针方向旋转，使边AB与AC重合得△ACD，BC的中点E的对应点为F，则∠EAF的度数为_______.

    60° 【解析】∵将等边△ABC绕顶点A顺时针方向旋转，使边AB与AC重合得△ACD，BC的中点E的对应点为F， ∴旋转角为60°，E，F是对应点， 则∠EAF的度数为：60°．

    查看答案和解析>>

    科目：初中数学 来源：安徽省蚌埠市2017届九年级下学期中考二模数学试卷 题型：解答题

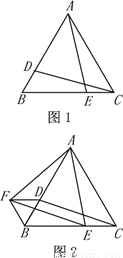
    如图1，图2，△ABC是等边三角形，D、E分别是AB、BC边上的两个动点（与点A、B、C不重合），始终保持BD=CE.

    （1）当点D、E运动到如图1所示的位置时,求证：CD=AE.

    （2）把图1中的△ACE绕着A点顺时针旋转60°到△ABF的位置（如图2），分别连结DF、EF.

    ①找出图中所有的等边三角形(△ABC除外)，并对其中一个给予证明；

    ②试判断四边形CDFE的形状,并说明理由.

    （1）证明见解析；（2）①图中有2个正三角形，分别是△BDF，△AFE，证明见解析；②四边形CDFE是平行四边形，理由见解析. 【解析】（1）∵△ABC是正三角形， ∴BC=CA，∠B=∠ECA=60°. …………………………（2分） 又∵BD=CE， ∴△BCD≌△CAE. …………………………（3分） ∴CD=AE. …………………………（4分） （2）① ...

    查看答案和解析>>

    科目：初中数学 来源：安徽省蚌埠市2017届九年级下学期中考二模数学试卷 题型：单选题

    一城市准备选购一千株高度大约为2米的某种风景树来进行街道绿化，有四个苗圃基地投标（单株树的价相同），采购小组从四个苗圃中任意抽查了20株树苗的高度，得到表中的数据. 你认为应选( )

    树苗平均高度

    标准差

    甲苗圃

    1.8

    0.2

    乙苗圃

    1.8

    0.6

    丙苗圃

    2.0

    0.6

    丁苗圃

    2.0

    0.2

    A. 甲苗圃的树 B. 乙苗圃的树苗 C. 丙苗圃的树苗 D. 丁苗圃的树苗

    D 【解析】试题解析：由于标准差和方差可以反映数据的波动大小，所以甲苗圃与丁苗圃比较合适； 又因为丁苗圃树苗平均高度大于甲苗圃，所以应选丁苗圃的树苗． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：2018人教版九年级数学下册练习：第二十七章 达标检测卷 题型：解答题

    如图，已知△ABC∽△ADE，AB=30cm，AD=18cm，BC=20cm，∠BAC=75°，∠ABC=40°．

    （1）求∠ADE和∠AED的度数；

    （2）求DE的长．

    （1）∠ADE=∠ABC=40°，∠AED=∠C=65°；（2）DE=12cm． 【解析】试题分析： 根据三角形的内角和定理求出，再根据相似三角形对应角相等解答； 根据相似三角形对应边成比例列式求解即可． 试题解析： 即 解得：

    查看答案和解析>>

    科目：初中数学 来源：2018人教版九年级数学下册练习：第二十七章 达标检测卷 题型：填空题

    已知△ABC∽△DEF ， 且它们的面积之比为4：9，则它们的相似比为________ ．

    2：3 【解析】因为S△ABC：S△DEF=4：9= ， 所以△ABC与△DEF的相似比为2：3， 故答案为：2：3．

    查看答案和解析>>

    科目：初中数学 来源：2018人教版九年级数学下册练习：第二十七章 达标检测卷 题型：单选题

    如图，在△ABC中，DE∥BC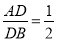， ，DE=4，则BC的长是（　　）

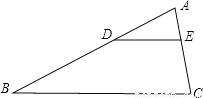
    A. 8 B. 10 C. 11 D. 12

    D 【解析】试题解析：∵， ∴， ∵在△ABC中，DE∥BC， ∴， ∵DE=4， ∴BC=3DE=12． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年甘肃省武威市凉州区洪祥镇九年级（上）期末数学试卷 题型：填空题

    已知圆锥的底面半径为3，侧面积为15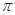，则这个圆锥的高为 ．

    4 【解析】试题分析：根据侧面积计算公式S=πrl，可得母线的长为5，则根据勾股定理可得h=4.

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级下册 期中测试卷 题型：解答题

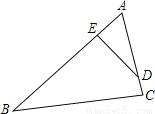
    为了估算河的宽度，我们可以在河对岸的岸边选定一个目标作为点A，再在河的这一边选点B和点C，使AB⊥BC，然后再选点E，使EC⊥BC，确定BC与AE的交点为D，如图．测得BD＝120米，DC＝60米，EC＝50米，你能求出两岸之间AB的大致距离吗？

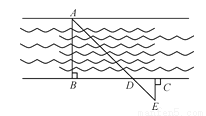
    100 【解析】试题分析： 由题意易证Rt△ABD∽Rt△ECD，结合题中的已知数据即可利用相似三角形对应边成比例解得AB的长. 试题解析： ∵AB⊥BC，EC⊥BC， ∴∠ABD＝∠ECD=90°， 又∵∠ADB＝∠EDC， ∴Rt△ABD∽Rt△ECD， ∴，即， ∴AB＝100. 答：两岸之间AB的大致距离为100米．

    查看答案和解析>>

    同步练习册答案