练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．当m＞-1时，抛物线y=（m-2）x2+（m-2）x+m+1与y轴的交点在x轴的上方．

    分析 根据抛物线y=（m-2）x2+（m-2）x+m+1与y轴的交点在x轴的上方得出c＞0，求得m的范围即可．

    解答 解：∵抛物线y=（m-2）x2+（m-2）x+m+1与y轴的交点在x轴的上方，
    ∴m+1＞0，
    ∴m＞-1，
    ∴m＞-1时，抛物线y=（m-2）x2+（m-2）x+m+1与y轴的交点在x轴的上方，
    故答案为＞-1．

    点评 本题考查了二次函数图象上点的坐标特征，掌握抛物线y=ax2+bx+c与y轴的交点在x轴的上方c＞0，是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    9．不等式$\left\{\begin{array}{l}{2x+4≤6}\\{x＞-3}\end{array}\right.$的解集在数轴上表示正确的是（　　）
    A．B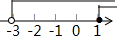．C．D．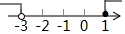

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．解不等式组$\left\{\begin{array}{l}{5x＞7x-10}\\{\frac{x}{3}≥1-\frac{x-3}{2}}\end{array}\right.$，并将解集在数轴上表示出来．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．不等式3-2x＞4x-9的正整数解是1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．操作：正方形ABCD的边长为4，P是直线CD上一动点，将三角尺的直角顶点与点P重合，一条直角边始终经过点B，另一直角边所在的直线与射线AD交于点E，设CP=x，DE=y．探究：
    （1）如图（1），当点P在正方形ABCD的边CD上时，求证：△BPC∽△PED；
    （2）当点P在CD的延长线上时，求y关于x的函数关系式；
    （3）当DE=1时，求点P的位置．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．在平面直角坐标系中，将点A（1，-1）向左平移4个单位长度得到点A'，点A'关于原点对称点的坐标是（3，1）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．已知m满足$\left\{\begin{array}{l}{2x+3y-m=0，}&{①}\\{3x+2y+1-m=0，}&{②}\end{array}\right.$且$\sqrt{x+y-199}$=-$\sqrt{199-x-y}$，求m的值．

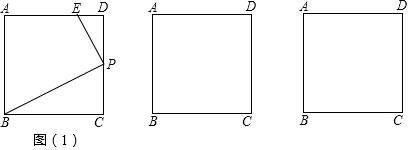
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．已知二次函数y=ax2-bx+0.5b-a与x轴交于A、B两点，则线段AB的最小值为（　　）
    A．0.5B．2C．$\sqrt{3}$D．无法确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

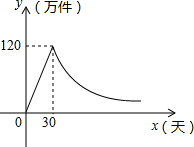    15．如图，某种商品上市之初采用了大量的广告宣传，其销售量与上市的天数之间成正比，当广告停止后，销售量与上市的天数之间成反比（如图所示），现己知上市30天时，当日销售量为120万件．
    （1）写出该商品上市以后销售量y（万件）与时间x（天数）之间的表达式；
    （2）求上市至第100天（含第100天），日销售量在36万件以下（不含36万件）的天数；
    （3）广告合同约定，当销售量不低于100万件，并且持续天数不少于10天时，广告设计师就可以拿到“特殊贡献奖”，本次广告策划，设计师能否拿到“特殊贡献奖”？

    查看答案和解析>>

    同步练习册答案