
����Ŀ����ͼ����������A��B���㣬�ֱ��Ӧ����Ϊa��b��| a |=3��| b |=9��
![]()
��1����a��b��ֵ��
��2������߶�AB�ij��ȡ�
��3������������һ��C����C��B�ľ�����C��A�����3����ֱ��д����C����ʾ������
��4����P�ӵ�A�������������ƶ�1����λ���ȣ��������ƶ�2����λ���ȣ��������ƶ�3����λ���ȣ��������ƶ�4����λ�������������������������1889���ƶ���ĵ�P����ʾ����
���𰸡���1��a=-3��b=9;��2��AB=12;��3��C����ʾ������0��-9;��4��-948
��������
��1��������õ���![]() ������
������![]() ������
������![]() ;
;
��2������֮��ij��ȣ���������֮�ʵľ��룬����![]() ��⣻
��⣻
��3��������������ۣ���C����AB֮��ʱ��![]() ����C��AB֮��ʱ��ֻ����A�����࣬
����C��AB֮��ʱ��ֻ����A�����࣬![]() ���ֱ������ɣ�
���ֱ������ɣ�
��4��1889���ƶ���ĵ�P����ʾ����Ϊ��![]() ��������ɡ�
��������ɡ�
�⣺��1���������֪��![]() ��
��
���ң�![]() ��
��
��![]() ;
;
��2��A���Ӧ������a
B���Ӧ������b��
��![]() ;
;
��3����C����AB֮��ʱ��
��![]()
![]()
��![]()
![]()
��![]() ��
��
��C��AB֮��ʱ��ֻ����A�����࣬
��![]()
�� ![]()
��![]()
����![]()
��![]()
����������C����ʾ������0��-9
��4��������ã�
![]()
![]()
![]()
![]()


 �¿α�����Ķ�ѵ��ϵ�д�
�¿α�����Ķ�ѵ��ϵ�д� ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������OABC��ƽ��ֱ������ϵ�ڵ�λ����ͼ��ʾ����OΪ����ԭ�㣬��A������Ϊ��10��0������B������Ϊ��10��8������ֱ֪��AC��˫����y��![]() ��m��0���ڵ�һ��������һ����Q��5��n����
��m��0���ڵ�һ��������һ����Q��5��n����
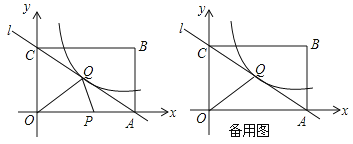
��1����ֱ��AC��˫���ߵĽ���ʽ��
��2��������P��A�������������AO��OC��·����ÿ��2����λ���ȵ��ٶ��˶�������C��ֹͣ�����OPQ�����S����˶�ʱ��t��ĺ�����ϵʽ������tȡ��ֵʱS��10��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����¸�ͼ������ͬ����С��ͼ�ٰ�һ��������ɣ����еڢٸ�ͼ���й���1���������Σ��ڢڸ�ͼ���й���5���������Σ��ڢ۸�ͼ���й���13���������Σ�������ڢ߸�ͼ�����������εĸ���Ϊ��������

A. 83B. 84C. 85D. 86
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ڡ�ABC�У���BAC=75������ACB=35������ABC��ƽ����BD����AC�ڵ�D��
��1����֤����BCDΪ���������Σ�
��2������BAC��ƽ����AE����BC�ڵ�E����ͼ2����֤��BD+AD=AB+BE��
��3������BAC��ǵ�ƽ����AE��CB�ӳ����ڵ�E������̽����2���еĽ����Ƿ���Ȼ������ֱ��д����ȷ�Ľ�����


ͼ1 ͼ2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
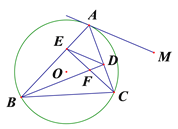
����Ŀ����ͼ����ABC�ǡ�O���ڽ������Σ�CE��AB�ڵ�E��BD��AC�ڵ�D��BD��CE�ཻ�ڵ�F������ED��
(1)����ABC=45��,֤��AE=EF��
(2)��֤����AED�ס�ACB��
(3)����A��ֱ��AM��ED�� AM�ǡ�O��������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
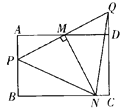
����Ŀ���ھ���ABCD�У�AB��8��AD��12��M��AD�ߵ��е㣬P��AB���ϵ�һ�����㣨����A��B�غϣ���PM���ӳ��߽�����CD��Q�㣬MN��PQ������BC��N�㡣
��1������N��BC֮��ʱ����ͼ��
����֤����NPQ����PQN��
������![]() �Ƿ�Ϊ��ֵ�����Ƕ�ֵ������ö�ֵ�������ǣ���ٷ���˵����
�Ƿ�Ϊ��ֵ�����Ƕ�ֵ������ö�ֵ�������ǣ���ٷ���˵����
��2������PBN����NCQ��������ʱ����AP��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
��1����5mn2��4m2n������2mn��
��2����x+7����x��6������x��2����x+1��
��3�� (��![]() )2 016��161 008��
)2 016��161 008��
���𰸡���1����10m2n3+8m3n2����2��2x��40��(3)1��
�������������������1��ԭʽ���õ���ʽ���Զ���ʽ������㼴�ɵõ������
��2��ԭʽ�������ö���ʽ���Զ���ʽ������㣬ȥ���źϲ����ɵõ������
��3���ȸ����ݵij˷��������㣬��(��![]() )2 016��Ϊ(
)2 016��Ϊ(![]() )1008���ٸ��ݻ��ij˷�����������㼴��.
)1008���ٸ��ݻ��ij˷�����������㼴��.
�����������1��ԭʽ=��5mn2������2mn��+����4m2n������2mn��=��10m2n3+8m3n2��
��2��ԭʽ=x2��6x+7x��42��x2��x+2x+2=2x��40��
��3��ԭʽ=(![]() )1008��161 008=(
)1008��161 008=(![]() ��16)1 008=1.
��16)1 008=1.
�����͡������
��������
19
����Ŀ����ͼ������ͼ��ÿ��С�����εı߳�Ϊ1����A��B��C���Ǹ�㣮
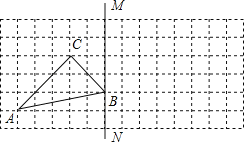
��1��������ABC����ֱ��BM�ԳƵ���A1B1C1��
��2��д��AA1�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
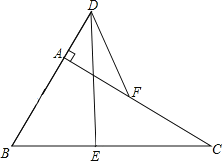
����Ŀ����ͼ����Rt��ABC�У���BAC=90�㣬E��F�ֱ���BC��AC���е㣬�ӳ�BA����D��ʹ2AD=AB������DE��DF��
��1����֤��AF��DE����ƽ�֣�
��2����BC=4����DF�ij���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com