
如图,在□ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6 ,AF=4
,AF=4 ,求AE的长.
,求AE的长.
(1)证明见解析;(2)6.
解析试题分析:(1)利用对应两角相等,证明两个三角形相似△ADF∽△DEC;
(2)利用△ADF∽△DEC,可以求出线段DE的长度;然后在在Rt△ADE中,利用勾股定理求出线段AE的长度.
(1)证明:∵?ABCD,∴AB∥CD,AD∥BC,
∴∠C+∠B=180°,∠ADF=∠DEC.
∵∠AFD+∠AFE=180°,∠AFE=∠B,
∴∠AFD=∠C.
在△ADF与△DEC中,
∴△ADF∽△DEC.
(2)∵△ADF∽△DEC,
∴
又 ∵ CD=AB=8,AD=6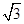 ,AF= 4
,AF= 4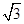 .
.
代入求得DE="12" ,
四边形ABCD是平行四边形,又∵AE⊥BC,∴ AE⊥AD,
在Rt△AED中,由勾股定理可得AE=6.
考点:1.相似三角形的判定与性质;2.勾股定理;3.平行四边形的性质.


科目:初中数学 来源: 题型:解答题
如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心,OA为半径的圆交AC于点D,E是BC的中点,连接DE,OE.
(1)判断DE与⊙O的位置关系,并说明理由;
(2)求证:BC2=2CD•OE;
(3)若cos∠BAD=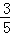 ,BE=
,BE=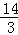 ,求OE的长.
,求OE的长.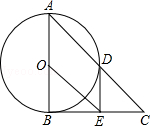
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,直线 =
= 分别与
分别与 轴,
轴, 轴相交于
轴相交于 两点,点
两点,点 是
是 轴的负半轴上的一个动点,以
轴的负半轴上的一个动点,以 为圆心,3为半径作
为圆心,3为半径作 .
.
(1)连结 ,若
,若 ,试判断
,试判断 与
与 轴的位置关系,并说明理由;
轴的位置关系,并说明理由;
(2)当 为何值时,以
为何值时,以 与直线
与直线 =
= 的两个交点和圆心
的两个交点和圆心 为顶点的三角形是正三角形?
为顶点的三角形是正三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图1,在△ABC中,D、E、F分别为三边的中点,G点在边AB上,且DG平分△ABC的周长,设BC=a、AC=b、AB=c.
(1)求线段BG的长;
(2)求证:DG平分∠EDF;
(3)连接CG,如图2,若△GBD ∽△GDF,求证:BG⊥CG.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在正方形ABCD中,E是BC上的一点,连结AE,作BF⊥AE,垂足为H,交CD于F,作CG∥AE,交BF于G.
求证:(1)CG=BH,
(2)FC2=BF·GF,
(3) =
= .
.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
操作:小明准备制作棱长为1cm的正方体纸盒,现选用一些废弃的圆形纸片进行如下设计:

说明:方案一:图形中的圆过点A、B、C;
方案二:直角三角形的两直角边与展开图左下角的正方形边重合,斜边经过两个正方形的顶点.
纸片利用率= ×100%
×100%
发现:(1)方案一中的点A、B恰好为该圆一直径的两个端点.
你认为小明的这个发现是否正确,请说明理由.
(2)小明通过计算,发现方案一中纸片的利用率仅约为38.2%.
请帮忙计算方案二的利用率,并写出求解过程.
探究:
(3)小明感觉上面两个方案的利用率均偏低,又进行了新的设计(方案三),请直接写出方案三的利用率.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知,如图1,矩形ABCD中,AD=6,DC=8,矩形EFGH的三个顶点E、G、H分别在矩形ABCD的边ABCD的边AB、CD、DA上,AH=2,连接CF.
(1)如图2,当四边形EFGH为正方形时,求CF的长和△FCG的面积;
(2)如图1,设AE=x,△FCG的面积=y,求y与x之间的函数关系式与y的最大值.
(3)当△CG是直角三角形时,求x和y值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com