
(10分)已知抛物线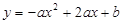 与
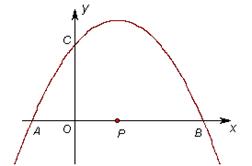
与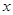 轴的一个交点为A(-1,0),与y轴的正半轴交于点C.
轴的一个交点为A(-1,0),与y轴的正半轴交于点C.
(1)直接写出抛物线的对称轴,及抛物线与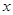 轴的另一个交点B的坐标;
轴的另一个交点B的坐标;
(2)当点C在以AB为直径的⊙P上时,求抛物线的解析式;
(3)坐标平面内是否存在点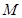 ,使得以点M和⑵中抛物线上的三点A、B、C为顶点的四边形是平行四边形?若存在,请求出点
,使得以点M和⑵中抛物线上的三点A、B、C为顶点的四边形是平行四边形?若存在,请求出点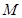 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
 |
见解析
【解析】
(1)根据对称轴公式,对称轴x=﹣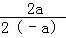 =1;
=1;
点B的坐标是(3,0).(2分)
(2)点C在以AB为直径的⊙P上,∴∠ACB=90°
由∠ACB=∠AOC=∠COB=90°得△AOC∽△COB,
∴ ,
,
∴CO= ,
,
∴b=
当x=﹣1,y=0时,﹣a﹣2a+ =0,
=0,
∴a=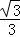 ,
,
∴y=﹣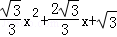 ;(6分)
;(6分)
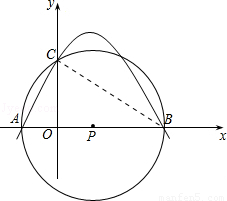
(3)点M的坐标有三种情况,如果以AB为平行四边形的对角线,那么P(1,0)就是平行四边开的对称中心,即C点与M点关于P点位对称,设M点坐标为(x,y).
那么 ,x=2 .
,x=2 . 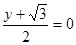 ,y=
,y= .∴M点坐标为(2,
.∴M点坐标为(2, )
)
同理以AC、BC为对称轴得出M点的坐标为(-4, )、(4,
)、(4, )
)
分别是:(2, ),(-4,
),(-4, )或(4,
)或(4, ).(10分)
).(10分)


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
(本题满分10分)已知抛物线![]() 与x轴有两个不同的交点.
与x轴有两个不同的交点.
1.(1) 求抛物线的对称轴;
2.(2) 求c的取值范围;
3.(3)若此抛物线与x轴两交点之间的距离为2,求c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
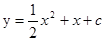 与x轴有两个不同的交点.
与x轴有两个不同的交点.查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(湖南衡阳卷)数学 题型:解答题
(2011湖南衡阳,27,10分)已知抛物线 .
.
(1)试说明:无论m为何实数,该抛物线与x轴总有两个不同的交点;
(2)如图,当该抛物线的对称轴为直线x=3时,抛物线的顶点为点C,直线y=x-1与抛物线交于A、B两点,并与它的对称轴交于点D.
①抛物线上是否存在一点P使得四边形ACPD是正方形?若存在,求出点P的坐标;若不存在,说明理由;
②平移直线CD,交直线AB于点M,交抛物线于点N,通过怎样的平移能使得C、D、M、N为顶点的四边形是平行四边形.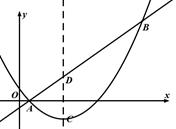
查看答案和解析>>
科目:初中数学 来源:2012届江苏省兴化市九年级上学期期末四校联考数学卷 题型:解答题
(本题满分10分)已知抛物线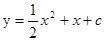 与x轴有两个不同的交点.
与x轴有两个不同的交点.
【小题1】(1) 求抛物线的对称轴;
【小题2】(2) 求c的取值范围;
【小题3】(3)若此抛物线与x轴两交点之间的距离为2,求c的值.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省兴化市九年级上学期期末四校联考数学卷 题型:解答题
(本题满分10分)已知抛物线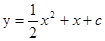 与x轴有两个不同的交点.
与x轴有两个不同的交点.
1.(1) 求抛物线的对称轴;
2.(2) 求c的取值范围;
3.(3)若此抛物线与x轴两交点之间的距离为2,求c的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com