
【题目】我国古代数学家刘徽发展了“重差术”,用于测量不可到达的物体的高度,比如,通过下列步骤可测量山的高度PQ(如图):
(1)测量者在水平线上的A处竖立一根竹竿,沿射线QA方向走到M处,测得山顶P、竹竿顶端B及M在一条直线上;
(2)将该竹竿竖立在射线QA上的C处,沿原方向继续走到N处,测得山顶P、竹竿顶端D及N在一条直线上;
(3)设竹竿与AM、CN的长分别为![]() 、a1、a2,可得公式:PQ=
、a1、a2,可得公式:PQ=![]() +
+![]() .则上述公式中,d表示的是( )
.则上述公式中,d表示的是( )
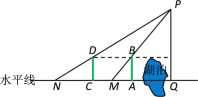
A. QA的长 B. AC的长 C. MN的长 D. QC的长
科目:初中数学 来源: 题型:
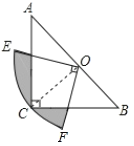
【题目】如图,在△ABC中,∠C=90°,AC=BC,斜边AB=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答下列各题
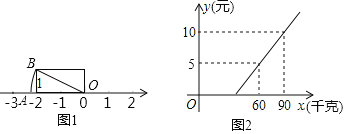
(1)如图1,已知OA=OB,数轴上的点A所表示的数为m,且|m+n|=2
①点A所表示的数m为 ;
②求代数式n2+m﹣9的值.
(2)旅客乘车按规定可以随身携带一定质量的行李,如果超过规定,则需购买行李票,设行李票y(元)是行李质量x(千克)的一次函数,其图象如图2所示.
①当旅客需要购买行李票时,求出y与x之间的函数关系式;
②如果张老师携带了42千克行李,她是否要购买行李票?如果购买需买多少行李票?
查看答案和解析>>
科目:初中数学 来源: 题型:
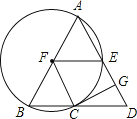
【题目】如图,在![]() 中,
中,![]() ,以AB为直径的
,以AB为直径的![]() 交BD于点C,交AD于点E,
交BD于点C,交AD于点E,![]() 于点G,连接FE,FC.
于点G,连接FE,FC.
![]() 求证:GC是
求证:GC是![]() 的切线;
的切线;
![]() 填空:
填空:
![]() 若
若![]() ,
,![]() ,则
,则![]() 的面积为______.
的面积为______.
![]() 当
当![]() 的度数为______时,四边形EFCD是菱形.
的度数为______时,四边形EFCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
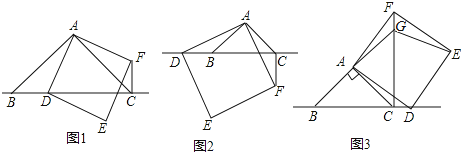
【题目】在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.
(1)观察猜想
如图1,当点D在线段BC上时,
①BC与CF的位置关系,
②BC,CD,CF之间的数量关系为;
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;
若不成立,请你写出正确结论再给予证明;
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2![]() ,CD=
,CD=![]() BC,求CF,EG.
BC,求CF,EG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.

(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1:y=2x+1与直线l2:y=mx+4相交于点P(1,b)
(1)求b,m的值
(2)垂直于x轴的直线x=a与直线l1,l2分别相交于C,D,若线段CD长为2,求a的值

查看答案和解析>>
科目:初中数学 来源: 题型:
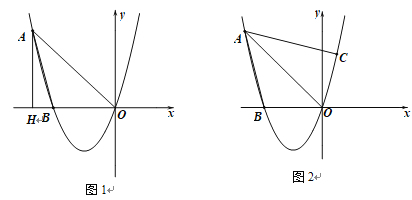
【题目】已知,经过点A(-4,4)的抛物线y=ax2+bx与x轴相交于点B(-3,0).
(1)求抛物线的解析式;
(2)如图1,过点A作AH⊥x轴,垂足为H,平行于y轴的直线交线段AO于点Q,交抛物线于点P,当四边形AHPQ为平行四边形时,求∠AOP的度数;
(3)如图2,,试探究:在抛物线上是否存在点C,使∠CAO=∠BAO?若存在,请求出直线AC解析式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(定义学习)
定义:如果四边形有一组对角为直角,那么我们称这样的四边形为“对直四边形”
(判断尝试)
在①梯形;②矩形:③菱形中,是“对直四边形”的是哪一个. (填序号)
(操作探究)
在菱形ABCD中,![]() 于点E,请在边AD和CD上各找一点F,使得以点A、E、C、F组成的四边形为“对直四边形”,画出示意图,并直接写出EF的长,
于点E,请在边AD和CD上各找一点F,使得以点A、E、C、F组成的四边形为“对直四边形”,画出示意图,并直接写出EF的长,

(实践应用)
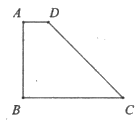
某加工厂有一批四边形板材,形状如图所示,若AB=3米,AD=1米,![]()
![]()
.现根据客户要求,需将每张四边形板材进一步分割成两个等腰三角形板材和一个“对直四边形"板材,且这两个等腰三角形的腰长相等,要求材料充分利用无剩余.求分割后得到的等腰三角形的腰长,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com