

分析 (1)①利用平行线的性质和三角形的外角即可;②利用平行线的特点作出平行线,再利用平行线的性质即可;
(2)利用三角形的外角等于与它不相邻的两内角的和即可;
(3)利用三角形的外角的性质把角转化到四边形CDHM中,用四边形的内角和即可.
解答 解:(1)①∵AB∥CD,
∴∠B=∠COP,
∵∠COP=∠BPD+∠D,
∴∠B=∠BPD+∠D,
即:∠BPD=∠B-∠D,
②不成立,
结论:∠BPD=∠B+∠D,
理由:如图b,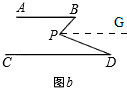
过点P作PG∥AB,
∴∠B=∠BPG,
∵PG∥AB,CD∥AB,
∴PG∥CD,
∴∠DPG=∠D,
∴∠BPD=∠BPG+∠DPG=∠B+∠D;
(2)结论:∠DPQ=∠B+∠BQD+∠D,
理由:如图c,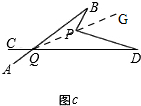
连接QP并延长,
∵∠BP∠G是△BPQ的外角,
∴∠BPG=∠B+∠BQP,
同理:∠DPG=∠D+∠DQP,
∴∠BPD=∠BPG+∠DPG=∠B+∠BQP+∠DQP+∠D=∠B+∠BQD+∠D;
(3)如图d,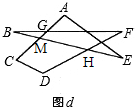
∵∠DHM是△BFH的外角,
∴∠DHM=∠B+∠F,
同理:∠CMH=∠A+∠E,
∴∠A+∠B+∠C+∠D+∠E+∠F=∠DHM+∠CMH+∠C+∠D=360°.
点评 此题是四边形的性质,主要考查了平行线的性质和判定,三角形的外角的性质,四边形的内角和,解本题的关键是作出辅助线,是一个比较简单也比较典型的中考常考题.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:选择题
| A. | a=-2 | B. | a>0 | C. | a=-2或a>0 | D. | a≤-2或a>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 图中的每个小正方形的边长均为1,每个小正方形的顶点叫做格点,线段AB和CD的端点A、B、C、D均在格点上.
图中的每个小正方形的边长均为1,每个小正方形的顶点叫做格点,线段AB和CD的端点A、B、C、D均在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 下面的长方体是由A,B,C,D四个选项中所示的四个几何体拼接而成的,而且这四个几何体都是由4个同样大小的正方体组成的,那么长方体中,第四部分所对应的几何体应是( )
下面的长方体是由A,B,C,D四个选项中所示的四个几何体拼接而成的,而且这四个几何体都是由4个同样大小的正方体组成的,那么长方体中,第四部分所对应的几何体应是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知如图,AD∥CF∥EB,AB=3,AC=5,DF=9,DA=2,CF=8,则,DE=$\frac{27}{5}$,EF=$\frac{18}{5}$,BE=4.
已知如图,AD∥CF∥EB,AB=3,AC=5,DF=9,DA=2,CF=8,则,DE=$\frac{27}{5}$,EF=$\frac{18}{5}$,BE=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com