
【题目】如图,抛物线![]() 与
与![]() 铀交于
铀交于![]() 两点(点
两点(点![]() 作点
作点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() 且
且![]() ,点
,点![]() 为抛物线
为抛物线![]() 的对称轴右侧图象上的一点.
的对称轴右侧图象上的一点.
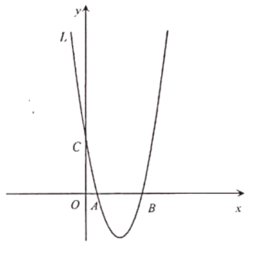
(1)a的值为_ ,抛物线的顶点坐标为_ ;
(2)设抛物线![]() 在点
在点![]() 和点
和点![]() 之间部分(含点
之间部分(含点![]() 和点
和点![]() )的最高点与最低点的纵坐标之差为
)的最高点与最低点的纵坐标之差为![]() ,求
,求![]() 关于
关于![]() 的函数表达式,并写出自变量
的函数表达式,并写出自变量![]() 的取值范围;
的取值范围;
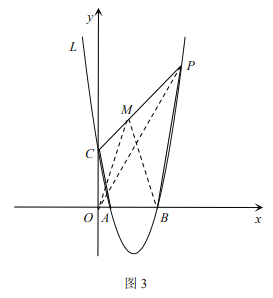
(3)当点![]() 的坐标满足:
的坐标满足:![]() 时,连接
时,连接![]() ,若
,若![]() 为线段
为线段![]() 上一点,且
上一点,且![]() 分四边形
分四边形![]() 的面积为相等两部分,求点
的面积为相等两部分,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时, ![]() 当
当![]() ,
,![]() ;(3)
;(3)![]()
【解析】
(1)根据抛物线![]() 与
与![]() 铀交于
铀交于![]() 两点(点
两点(点![]() 作点
作点![]() 的左侧),可得A点坐标为:(1,0),B点坐标为:(5,0),
的左侧),可得A点坐标为:(1,0),B点坐标为:(5,0),![]() ,则有C点坐标为:(0,5),可得
,则有C点坐标为:(0,5),可得![]() ,抛物线
,抛物线![]() 的函数表达式为:
的函数表达式为:![]() ,得到抛物线的顶点坐标为(3,-4);
,得到抛物线的顶点坐标为(3,-4);
(2)根据抛物线![]() 的函数表达式为:
的函数表达式为:![]() ,得到抛物线
,得到抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,分两种情况:当
,分两种情况:当![]() 时,点
时,点![]() 为最高点,抛物线
为最高点,抛物线![]() 的顶点为最低点,当
的顶点为最低点,当![]() 时,点
时,点![]() 为最高点,抛物线
为最高点,抛物线![]() 的顶点为最低点,分别求出h的函数表达式即可;
的顶点为最低点,分别求出h的函数表达式即可;
(3)根据点![]() (
(![]() )是抛物线
)是抛物线![]() 图象上的点,
图象上的点,![]() ,可得方程
,可得方程![]() ,解得
,解得![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,设直线
,设直线![]() 的函数表达式为
的函数表达式为![]() ,代入P,C两点坐标可求得
,代入P,C两点坐标可求得![]() ,设点
,设点![]() 的坐标为
的坐标为![]() ,利用
,利用![]() 分四边形
分四边形![]() 的面积为相等两部分,即:
的面积为相等两部分,即:![]() ,可得
,可得![]() ,解得
,解得![]() ,
,![]() ,可得点
,可得点![]() 的坐标为
的坐标为![]() .
.
解:(1)∵抛物线![]() 与
与![]() 铀交于
铀交于![]() 两点(点
两点(点![]() 作点
作点![]() 的左侧),
的左侧),
∴A点坐标为:(1,0),B点坐标为:(5,0),
∴![]()
∴C点坐标为:(0,5),
即:![]()
∴![]() ,
,
∴抛物线![]() 的函数表达式为:
的函数表达式为:![]() ,
,
∴抛物线的顶点坐标为(3,-4);
(2)由(1)可知:抛物线![]() 的函数表达式为:
的函数表达式为:![]()
![]() 当
当![]() 时,
时,![]() ,
,
![]() .
.
抛物线![]() 的对称轴为直线
的对称轴为直线![]() .
.
当![]() 时,点
时,点![]() 为最高点,抛物线
为最高点,抛物线![]() 的顶点为最低点,
的顶点为最低点,
![]()
当![]() 时,点
时,点![]() 为最高点,抛物线
为最高点,抛物线![]() 的顶点为最低点,
的顶点为最低点,
![]()
(3)∵点![]() (
(![]() )是抛物线
)是抛物线![]() 图象上的点,
图象上的点,
![]()
又![]() ,
,
![]()
![]()
即![]()
![]() (舍),
(舍),
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
设直线![]() 的函数表达式为
的函数表达式为![]()
![]() ,
,
解得![]()
![]() .
.
设点![]() 的坐标为
的坐标为![]() ,
,
连接![]()
![]()
![]()
![]()
解得![]()
![]()
![]() 点
点![]() 的坐标为
的坐标为![]() .
.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的关系如图所示.根据图象所提供的信息有:①甲队挖掘30m时,用了3h;②挖掘6h时甲队比乙队多挖了10m;③乙队的挖掘速度总是小于甲队;④开挖后甲、乙两队所挖河渠长度相等时,x=4.其中一定正确的有( )
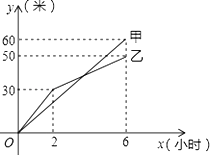
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
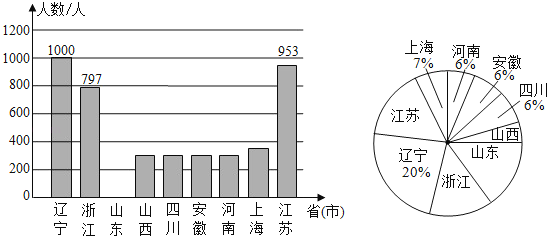
【题目】2020年春节前夕“新型冠状病毒”爆发,疫情就是命令,防控就是使命.全国各地驰援武汉的医护工作者,践行医者仁心的使命与担当,舍小家,为大家,用自己的专业知识与血肉之躯构筑起全社会抗击疫情的钢铁长城.下面是2月9日当天全国部分省市驰援武汉医护工作者的人数统计图(不完整).
请解答下列问题:
(1)①上述省市2月9日当天驰援武汉的医护工作者的总人数为 人;
②请将条形统计图补充完整;
(2)请求出扇形统计图中“山东”所对应扇形的圆心角的度数;
(3)本次山东驰援武汉的医护工作者中,有5人报名去重症区,王医生和李医生就在其中,若从报名的5人中随机安排2人,求同时安排王医生和李医生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大邑县某汽车出租公司有若干辆同一型号的货车对外出租,每辆货车的日租金实行淡季、旺季两种价格标准,旺季每辆货车的日租金比淡季上涨25%.据统计,淡季该公司平均每天有10辆货车未出租,日租金总收入为3200元;旺季所有的货车每天能全部租出,日租金总收入为6000元.
(1)求该出租公司这批对外出租的货车共有多少辆?
(2)经市场调查发现,在旺季如果每辆货车的日租金每上涨20元,每天租出去的货车就会减少1辆,不考虑其它因素,该出租公司的日租金总收入最高是多少元?当日租金总收入最高时,每天出租货车多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点![]() 是数轴上:从左到右排列的三个点,分别对应的数为
是数轴上:从左到右排列的三个点,分别对应的数为![]() 某同学将刻度尺如图2放置.使刻度尺上的数字
某同学将刻度尺如图2放置.使刻度尺上的数字![]() 对齐数轴上的点
对齐数轴上的点![]() ,发现点
,发现点![]() 对齐刻度
对齐刻度![]() ,点
,点![]() 对齐刻度
对齐刻度![]() .
.
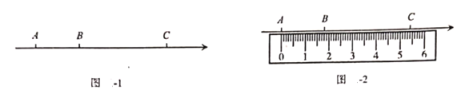
(1)在图1的数轴上,![]() 个单位长度;数轴上的一个单位长度对应刻度尺上的
个单位长度;数轴上的一个单位长度对应刻度尺上的 ![]() .
.
(2)求数轴上点![]() 所对应的数
所对应的数![]() ;
;
(3)在图1的数轴上,点![]() 是线段
是线段![]() 上一点,满足
上一点,满足![]() 求点
求点![]() 所表示的数.
所表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了增强中学生的体质,某校食堂每天都为学生提供一定数量的水果,学校李老师为了了解学生喜欢吃哪种水果,进行了抽样调查,调查分为五种类型:A喜欢吃苹果的学生;B喜欢吃桔子的学生;C.喜欢吃梨的学生;D.喜欢吃香蕉的学生;E喜欢吃西瓜的学生,并将调查结果绘制成图1和图2 的统计图(不完整).请根据图中提供的数据解答下列问题:

(1)求此次抽查的学生人数;
(2)将图2补充完整,并求图1中的![]() ;
;
(3)现有5名学生,其中A类型2名,B类型2名,从中任选2名学生参加很体能测试,求这两名学生为同一类型的概率(用列表法或树状图法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】天门山索道是世界最长的高山客运索道,位于张家界天门山景区.在一次检修维护中,检修人员从索道A处开始,沿A﹣B﹣C路线对索道进行检修维护.如图:已知![]() 米,
米,![]() 米,AB与水平线
米,AB与水平线![]() 的夹角是
的夹角是![]() ,BC与水平线
,BC与水平线![]() 的夹角是
的夹角是![]() .求:本次检修中,检修人员上升的垂直高度
.求:本次检修中,检修人员上升的垂直高度![]() 是多少米?(结果精确到1米,参考数据:
是多少米?(结果精确到1米,参考数据:![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() 是平面内不与点
是平面内不与点![]() 重合的任意一点,连接
重合的任意一点,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点.
的中点.
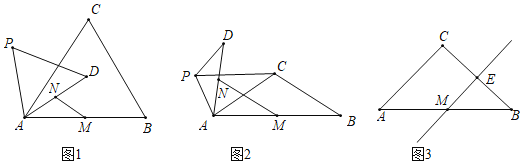
(1)问题发现:
如图1,当![]() 时,
时,![]() 的值是_________,直线
的值是_________,直线![]() 与直线
与直线![]() 相交所成的较小角的度数是________.
相交所成的较小角的度数是________.
(2)类比探究:
如图2,当![]() 时,请写出
时,请写出![]() 的值及直线
的值及直线![]() 与直线
与直线![]() 相交所成的较小角的度数,并说明理由.
相交所成的较小角的度数,并说明理由.
(3)解决问题:
如图3,当![]() 时,若
时,若![]() 是
是![]() 的中点,点
的中点,点![]() 在直线
在直线![]() 上,且点
上,且点![]() 在同一条直线上,请直接写出
在同一条直线上,请直接写出![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com