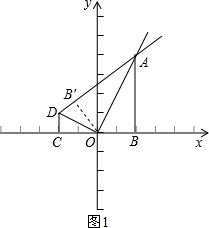
解:(1)在AD上截取AB′=AB,连接OB′.如图1所示:
∵A(2,4),∴OB=2,AB=4.
∵将△AOB沿AO翻折得到△AOB′,
∴AB′=AB=4,OB′=OB=2,OB′⊥AD.
∵OA⊥OD,OB′⊥AD,
∴∠OB′D=∠OB′A=90°,
∴∠B′DO+∠DOB′=90°,∠B′DO+∠OAD=90°,
∴∠DOB′=∠OAD,
∴△OB′D∽△AB′O,
∴OB′
2=AB′•DB′,即2
2=4DB′,
∴DB′=1.
在直角△ODB′中,根据勾股定理得:OD=

.
∵∠AOD=90°,∴∠DOC+∠AOB=90°,
又∠DCO=90°,∴∠CDO+∠DOC=90°,
∴∠AOB=∠CDO,
∴△CDO∽△BOA,
∴
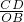
=

=

,即
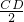
=
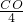
=
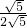
,
∴CD=1,CO=2,即D(-2,1).
设直线AD的解析式为y=kx+b,将A和D的坐标代入,
得:
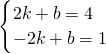
,
解得:
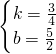
,
故直线AD的解析式为y=

x+

;

(2)分两种情况:
①如果动点P在线段OA上时,0≤t≤2.如图2①所示:
∵OP=

t,OA=2

,∴AP=OA-OP=2

-

t.
∵PE∥AB,∴PE:AB=OE:OB=OP:OA,
∴PE:4=OE:2=

t:2

=t:2,
∴PE=2t,OE=t.
易证△MAP≌△QAP,则PM=PQ.
∵PM∥OD,∴PM:OD=AP:OA,
∴PM:

=(2

-

t):2

,
∴PM=

AP=

(2

-

t),
∴PQ=PM=

(2

-

t).
过点P作PE⊥BC于E.
∵BQ∥EP∥CN,
∴PQ:PN=BE:CE,
∴

(2

-

t):PN=(2-t):(2+t),
∴PN=

(2+t),
∴s=

AP•PN=

(2

-

t)×

(2+t)=

(4-t
2);
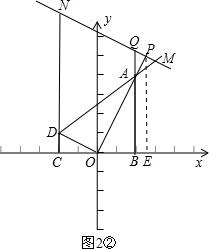
②如果动点P在射线OA上时,t>2.如图2②所示:
∵OP=

t,OA=2

,∴AP=OP-OA=

t-2

.
∵PE∥AB,∴PE:AB=OE:OB=OP:OA,
∴PE:4=OE:2=

t:2

=t:2,
∴PE=2t,OE=t.
易证△MAP≌△QAP,则PM=PQ.
∵PM∥OD,∴PM:OD=AP:OA,
∴PM:

=(

t-2

):2

,
∴PM=

AP=

(

t-2

),
∴PQ=PM=

(

t-2

).
过点P作PE⊥BC于E.
∵BQ∥EP∥CN,
∴PQ:PN=BE:CE,
∴

(

t-2

):PN=(t-2):(t+2),
∴PN=

(t+2),
∴s=

AP•PN=

(

t-2

)×

(t+2)=

(t
2-4).
综上,可知s=
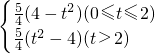
;
(3)在动点P运动的过程中,存在t=

或

,使NQ=3MP.理由如下:
分两种情况:
①如果动点P在线段OA上时,0≤t≤2.
∵NQ=3MP,MP=PQ,
∴PN=2PQ,
又∵PN=

(2+t),PQ=

(2

-

t),
∴

(2+t)=2×

(2

-

t),
∴t=

,符合题意;
②如果动点P在射线OA上时,t>2.
∵NQ=3MP,MP=PQ,
∴PN=4PQ,
又∵PN=

(t+2),PQ=

(

t-2

),
∴

(t+2)=4×

(

t-2

),
∴t=

,符合题意.
故在动点P运动的过程中,存在t=

或

,使NQ=3MP.
分析:(1)在AD上截取AB′=AB,连接OB′,先由轴对称的性质得出AB′=AB=4,OB′=OB=2,OB′⊥AD,再证明△OB′D∽△AB′O,根据相似三角形对应边成比例,得出DB′=1,则OD=

,再证明△CDO∽△BOA,得出D(-2,1),然后运用待定系数法即可求出直线AD的解析式;
(2)分两种情况:①动点P在线段OA上;②动点P在射线OA上.对于①,画出图形,由于△ANP的面积s=

AP•PN,而AP=OA-OP=2

-

t,所以关键是用含t的代数式表示PN.先由ASA得出△MAP≌△QAP,则PM=PQ,再由PM∥OD,得出PM=

AP=

(2

-

t).然后过点P作PE⊥BC于E,由平行线分线段成比例定理,可得PQ:PN=BE:CE,从而求出PN;对于②,同①可求;
(3)分两种情况:①动点P在线段OA上时,则有PN=2PQ,据此列出关于t的方程;②动点P在射线OA上时,则有PN=4PQ,据此列出关于t的方程.如果求出的t值经检验,符合题意,则存在;否则,不存在.
点评:本题主要考查了轴对称的性质,相似三角形的判定与性质,平行线分线段成比例定理,以及一次函数的综合应用,要注意的是(2)与(3)中,要根据P点的不同位置进行分类求解.

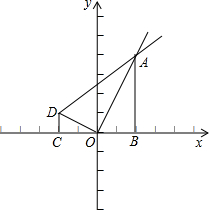 △AOB′,OD⊥OA交直线AB′于点D,CD⊥x轴于点C.
△AOB′,OD⊥OA交直线AB′于点D,CD⊥x轴于点C. 个单位的速度沿着射线OA运动,过点P作OA的垂线,与直线AB、AD、CD分别交于点Q、M、N,连接NA,设动点P的运动时间为t,△ANP的面积为s,求s与t的函数关系式;
个单位的速度沿着射线OA运动,过点P作OA的垂线,与直线AB、AD、CD分别交于点Q、M、N,连接NA,设动点P的运动时间为t,△ANP的面积为s,求s与t的函数关系式;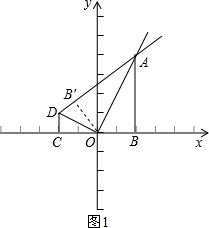 解:(1)在AD上截取AB′=AB,连接OB′.如图1所示:
解:(1)在AD上截取AB′=AB,连接OB′.如图1所示: .
.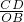 =
= =
= ,即
,即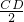 =
=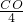 =
=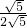 ,
,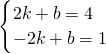 ,
,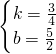 ,
, x+
x+ ;
;
 t,OA=2
t,OA=2 ,∴AP=OA-OP=2
,∴AP=OA-OP=2 -
- t.
t. t:2
t:2 =t:2,
=t:2, =(2
=(2 -
- t):2
t):2 ,
, AP=
AP= (2
(2 -
- t),
t), (2
(2 -
- t).
t). (2
(2 -
- t):PN=(2-t):(2+t),
t):PN=(2-t):(2+t), (2+t),
(2+t), AP•PN=
AP•PN= (2
(2 -
- t)×
t)× (2+t)=
(2+t)= (4-t2);
(4-t2); ②如果动点P在射线OA上时,t>2.如图2②所示:
②如果动点P在射线OA上时,t>2.如图2②所示: t,OA=2
t,OA=2 ,∴AP=OP-OA=
,∴AP=OP-OA= t-2
t-2 .
. t:2
t:2 =t:2,
=t:2, =(
=( t-2
t-2 ):2
):2 ,
, AP=
AP= (
( t-2
t-2 ),
), (
( t-2
t-2 ).
). (
( t-2
t-2 ):PN=(t-2):(t+2),
):PN=(t-2):(t+2), (t+2),
(t+2), AP•PN=
AP•PN= (
( t-2
t-2 )×
)× (t+2)=
(t+2)= (t2-4).
(t2-4).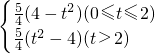 ;
; 或
或 ,使NQ=3MP.理由如下:
,使NQ=3MP.理由如下: (2+t),PQ=
(2+t),PQ= (2
(2 -
- t),
t), (2+t)=2×
(2+t)=2× (2
(2 -
- t),
t), ,符合题意;
,符合题意; (t+2),PQ=
(t+2),PQ= (
( t-2
t-2 ),
), (t+2)=4×
(t+2)=4× (
( t-2
t-2 ),
), ,符合题意.
,符合题意. 或
或 ,使NQ=3MP.
,使NQ=3MP. ,再证明△CDO∽△BOA,得出D(-2,1),然后运用待定系数法即可求出直线AD的解析式;
,再证明△CDO∽△BOA,得出D(-2,1),然后运用待定系数法即可求出直线AD的解析式; AP•PN,而AP=OA-OP=2
AP•PN,而AP=OA-OP=2 -
- t,所以关键是用含t的代数式表示PN.先由ASA得出△MAP≌△QAP,则PM=PQ,再由PM∥OD,得出PM=
t,所以关键是用含t的代数式表示PN.先由ASA得出△MAP≌△QAP,则PM=PQ,再由PM∥OD,得出PM= AP=
AP= (2
(2 -
- t).然后过点P作PE⊥BC于E,由平行线分线段成比例定理,可得PQ:PN=BE:CE,从而求出PN;对于②,同①可求;
t).然后过点P作PE⊥BC于E,由平行线分线段成比例定理,可得PQ:PN=BE:CE,从而求出PN;对于②,同①可求;

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
 如图,在平面直角坐标中,已知直线y=kx+b与直线y=
如图,在平面直角坐标中,已知直线y=kx+b与直线y= 如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数y=
如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数y=