
在平面直角坐标系xOy中,点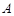 、
、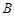 分别在
分别在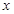 轴、
轴、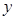 轴的正半轴上,且
轴的正半轴上,且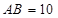 ,点
,点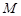 为线段
为线段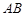 的中点.
的中点.
(1)如图1,线段 的长度为________________;
的长度为________________;
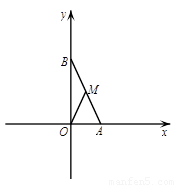
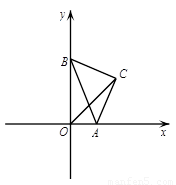
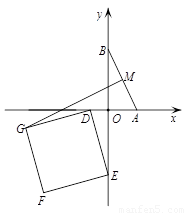
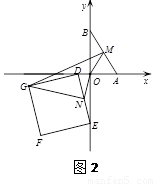
(2)如图2,以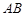 为斜边作等腰直角三角形
为斜边作等腰直角三角形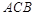 ,当点
,当点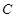 在第一象限时,求直线
在第一象限时,求直线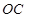 所对应的函数的解析式;
所对应的函数的解析式;
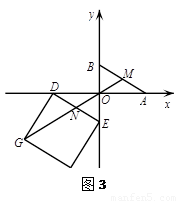
(3)如图3,设点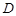 、
、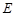 分别在
分别在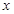 轴、
轴、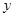 轴的负半轴上,且
轴的负半轴上,且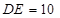 ,以
,以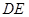 为边在第三象限内作正方形
为边在第三象限内作正方形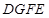 ,请求出线段
,请求出线段 长度的最大值,并直接写出此时直线
长度的最大值,并直接写出此时直线 所对应的函数的解析式.
所对应的函数的解析式.
(1)5 (2)直线OC所对应的函数解析式为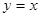 (3)线段MG取最大值10+
(3)线段MG取最大值10+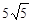 .
.
此时直线MG的解析式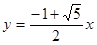
【解析】
试题分析:(1)根据直角三角形的斜边中线等于斜边的一半得线段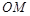 的长度为5.
的长度为5.
以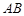 为斜边作等腰直角三角形
为斜边作等腰直角三角形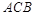 ,当点
,当点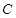 在第一象限时,过点C分别作CP⊥x轴于P,CQ⊥y轴于Q.
在第一象限时,过点C分别作CP⊥x轴于P,CQ⊥y轴于Q.
所以∠CQB=∠CPA=90°,又有∠QOP=90°,∠QCP=90°.∠BCA=90°,∠BCQ=∠ACP.BC=AC,
可证得△BCQ≌△ACP.从而得CQ=CP.不妨设C点的坐标为(a,a)(其中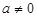 ).
).
设直线OC所对应的函数解析式为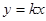 ,
,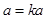 ,解得k=1,所以直线OC所对应的函数解析式为
,解得k=1,所以直线OC所对应的函数解析式为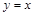 (3)取DE的中点N,连结ON、NG、OM.因为∠AOB=90°,所以OM=
(3)取DE的中点N,连结ON、NG、OM.因为∠AOB=90°,所以OM=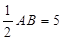 .同理得ON=5.
.同理得ON=5.
在正方形DGFE,N为DE中点,DE=10,由勾股定理得NG=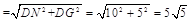 .在点M与G之间总有
.在点M与G之间总有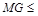 MO+ON+NG由于∠DNG的大小为定值,只要
MO+ON+NG由于∠DNG的大小为定值,只要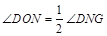 ,且M、N关于点O中心对称时,M、O、N、G四点共线,此时等号成立.这时线段MG取最大值10+
,且M、N关于点O中心对称时,M、O、N、G四点共线,此时等号成立.这时线段MG取最大值10+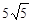 .
.
此时直线MG的解析式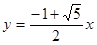
试题解析:(1)5
(2)如图1,过点C分别作CP⊥x轴于P,CQ⊥y轴于Q.
∴∠CQB=∠CPA=90°,
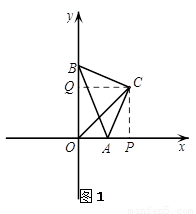
∵∠QOP=90°,
∴∠QCP=90°.
∵∠BCA=90°,
∴∠BCQ=∠ACP.
∵BC=AC,
∴△BCQ≌△ACP.
∴CQ=CP.
∵点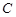 在第一象限,
在第一象限,
∴不妨设C点的坐标为(a,a)(其中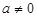 ).
).
设直线OC所对应的函数解析式为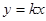 ,
,
∴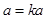 ,解得k=1,
,解得k=1,
∴直线OC所对应的函数解析式为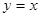 .
4分
.
4分
(3)取DE的中点N,连结ON、NG、OM.
∵∠AOB=90°,
∴OM=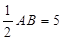 .
.
同理ON=5.
∵正方形DGFE,N为DE中点,DE=10,
∴NG=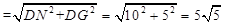 .
.
在点M与G之间总有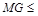 MO+ON+NG(如图2),
MO+ON+NG(如图2),
由于∠DNG的大小为定值,只要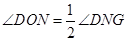 ,且M、N关于点O中心对称时,M、O、N、G四点共线,此时等号成立(如图3).
,且M、N关于点O中心对称时,M、O、N、G四点共线,此时等号成立(如图3).
∴线段MG取最大值10+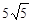 .
.
此时直线MG的解析式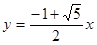
考点:1.直角三角形斜边中线等于斜边一半,2.在直角坐标系中求点的坐标,3.待定系数法求一次函数解析式.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.
如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为
如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com