Question

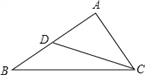
【题目】如图，已知在△ABC中，D是AB的中点，且∠ACD=∠B，若 AB=10，求AC的长．

【答案】5.

【解析】试题分析：

由点D是AB的中点，AB=10，易得AD=5；再由∠ACD=∠B，∠A=∠A，可证得：

△ACD∽△ABC，从而可得： ，由此得到：AC2=ADAB=50即可解得AC的值.

试题解析：

∵∠ACD=∠B，∠A=∠A，

∴△ACD∽△ABC．

∴，

∴AC2=ADAB.

∵D是AB的中点，AB=10，

∴AD=AB=5,

∴AC2=50．

解得AC=.

【题型】解答题
【结束】
22

【题目】口袋中装有四个大小完全相同的小球，把它们分别标号1,2,3,4，从中随机摸出一个球，记下数字后放回，再从中随机摸出一个球，利用树状图或者表格求出两次摸到的小球数和等于4的概率.

Answer 1

【答案】 .

【解析】试题分析：

根据题意列表如下，由表可以得到所有的等可能结果，再求出所有结果中，两次所摸到小球的数字之和为4的次数，即可计算得到所求概率.

试题解析：

列表如下：

	1	2	3	4
1	（1，1）	（1，2）	（1，3）	（1，4）
2	（2，1）	（2，2）	（2，3）	（2，4）
3	（3，1）	（3，2）	（3，3）	（3，4）
4	（4，1）	（4，2）	（4，3）	（4，4）

由表可知，共有16种等可能事件，其中两次摸到的小球数字之和等于4的有（3，1）、（2，2）和（1，3），共计3种，

∴P（两次摸到小球的数字之和等于4）=.