
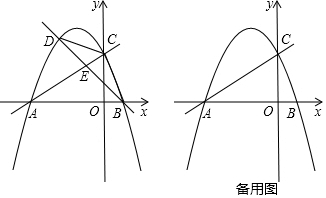
分析 (1)根据题意得到A(-4,0),C(0,2)代入y=-$\frac{1}{2}$x2+bx+c,于是得到结论;
(2)①如图,令y=0,解方程得到x1=-4,x2=1,求得B(1,0),过D作DM⊥x轴于M,过B作BN⊥x轴交于AC于N,根据相似三角形的性质即可得到结论;
②根据勾股定理的逆定理得到△ABC是以∠ACB为直角的直角三角形,取AB的中点P,求得P(-$\frac{3}{2}$,0),得到PA=PC=PB=$\frac{5}{2}$,过D作x轴的平行线交y轴于R,交AC的延线于G,情况一:如图,∠DCF=2∠BAC=∠DGC+∠CDG,情况二,∠FDC=2∠BAC,解直角三角形即可得到结论.
解答 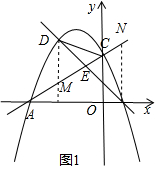 解:(1)根据题意得A(-4,0),C(0,2),
解:(1)根据题意得A(-4,0),C(0,2),
∵抛物线y=-$\frac{1}{2}$x2+bx+c经过A、C两点,
∴$\left\{\begin{array}{l}{0=-\frac{1}{2}×16-4b+c}\\{2=c}\end{array}\right.$,
∴$\left\{\begin{array}{l}{b=-\frac{3}{2}}\\{c=2}\end{array}\right.$,
∴y=-$\frac{1}{2}$x2-$\frac{3}{2}$x+2;
(2)①如图,令y=0,
∴-$\frac{1}{2}$x2-$\frac{3}{2}$x+2=0,
∴x1=-4,x2=1,
∴B(1,0),
过D作DM⊥x轴交AC于点M,过B作BN⊥x轴交于AC于N,
∴DM∥BN,
∴△DME∽△BNE,
∴$\frac{S_1}{S_2}$=$\frac{DE}{BE}$=$\frac{DM}{BN}$,
设D(a,-$\frac{1}{2}$a2-$\frac{3}{2}$a+2),
∴M(a,$\frac{1}{2}$a+2),
∵B(1,0),
∴N(1,$\frac{5}{2}$),
∴$\frac{S_1}{S_2}$=$\frac{DM}{BN}$=$\frac{-\frac{1}{2}{a}^{2}-2a}{\frac{5}{2}}=-\frac{1}{5}$(a+2)2+$\frac{4}{5}$;
∴当a=-2时,$\frac{S_1}{S_2}$的最大值是$\frac{4}{5}$;
②∵A(-4,0),B(1,0),C(0,2),
∴AC=2$\sqrt{5}$,BC=$\sqrt{5}$,AB=5,
∴AC2+BC2=AB2,
∴△ABC是以∠ACB为直角的直角三角形,取AB的中点P,
∴P(-$\frac{3}{2}$,0),
∴PA=PC=PB=$\frac{5}{2}$,
∴∠CPO=2∠BAC,
∴tan∠CPO=tan(2∠BAC)=$\frac{4}{3}$,
过D作x轴的平行线交y轴于R,交AC的延长线于G,
情况一:如图,∴∠DCF=2∠BAC=∠DGC+∠CDG,
∴∠CDG=∠BAC,
∴tan∠CDG=tan∠BAC=$\frac{1}{2}$,
即$\frac{RC}{DR}=\frac{1}{2}$,
令D(a,-$\frac{1}{2}$a2-$\frac{3}{2}$a+2),
∴DR=-a,RC=-$\frac{1}{2}$a2-$\frac{3}{2}$a,
∴$\frac{-\frac{1}{2}{a}^{2}-\frac{3}{2}a}{-a}=\frac{1}{2}$,
∴a1=0(舍去),a2=-2,
∴xD=-2,
情况二,∴∠FDC=2∠BAC,
∴tan∠FDC=$\frac{4}{3}$,
设FC=4k,
∴DF=3k,DC=5k,
∵tan∠DGC=$\frac{3k}{FG}$=$\frac{1}{2}$,
∴FG=6k,
∴CG=2k,DG=3$\sqrt{5}$k,
∴RC=$\frac{2\sqrt{5}}{5}$k,RG=$\frac{4\sqrt{5}}{5}$k,
DR=3$\sqrt{5}$k-$\frac{4\sqrt{5}}{5}$k=$\frac{11\sqrt{5}}{5}$k,
∴$\frac{DR}{RC}$=$\frac{\frac{11\sqrt{5}}{5}k}{\frac{2\sqrt{5}}{5}k}$=$\frac{-a}{-\frac{1}{2}{a}^{2}-\frac{3}{2}a}$,
∴a1=0(舍去),a2=-$\frac{29}{11}$,
点D的横坐标为-2或-$\frac{29}{11}$.
点评 本题考查了待定系数法求函数的解析式,相似三角形的判定和性质,解直角三角形,直角三角形的性质,正确的作出辅助线是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
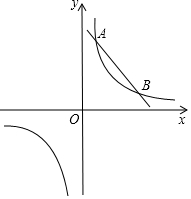 如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$的图形交于A(a,4)和B(4,1)两点.
如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$的图形交于A(a,4)和B(4,1)两点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
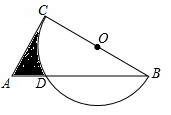 如图,Rt△ABC中,∠ACB=90°,AB=6,AC=3,以BC为直径的半圆交AB于点D,则阴影部分的面积为$\frac{45}{16}$$\sqrt{3}$+$\frac{9π}{80}$.
如图,Rt△ABC中,∠ACB=90°,AB=6,AC=3,以BC为直径的半圆交AB于点D,则阴影部分的面积为$\frac{45}{16}$$\sqrt{3}$+$\frac{9π}{80}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在矩形ABCD中,点E,F分别是AD,BC边上的点,且AE=CF.
如图,在矩形ABCD中,点E,F分别是AD,BC边上的点,且AE=CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠A>∠B.
如图,在△ABC中,∠A>∠B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com