三通管的立体图如图所示.则这个几何体的主视图是( )A．B．C．D．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

9．

三通管的立体图如图所示，则这个几何体的主视图是（　　）

A．

B．

C．

D．

分析根据从正面看得到的图形是主视图，可得答案．

解答解：从正面看是一个倒写的“T”字，
故选：B．

点评本题考查了简单组合体的三视图，从正面看得到的图形是主视图．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：选择题

19．下列运算中，计算结果正确的是（　　）

A．

a²•a³=a⁶

B．

a²+a³=a⁵

C．

（a²）³=a⁶

D．

a¹²÷a⁶=a²

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

20．【问题提出】
已知任意三角形的两边及夹角（是锐角），求三角形的面积．
【问题探究】
为了解决上述问题，让我们从特殊到一般展开探究．
探究一：在Rt△ABC（图1）中，∠ABC=90°，AC=b，BC=a，∠C=α，求△ABC的面积（用含a、b、α的代数式表示）
在Rt△ABC中，∠ABC=90°
∴sinα=$\frac{AB}{AC}$
∴AB=b•sinα
∴S_△ABC=$\frac{1}{2}$BC•AB=$\frac{1}{2}$absinα
探究二：
锐角△ABC（图2）中，AC=b，BC=a，∠C=α（0°＜α＜90°）
求：△ABC的面积．（用含a、b、α的代数式表示）
探究三：
钝角△ABC（图3）中，AC=b，BC=a，∠C=α（0°＜α＜90°）
求：△ABC的面积．（用含a、b、α的代数式表示）
【问题解决】
用文字叙述：已知任意三角形的两边及夹角（是锐角），求三角形面积的方法是S=$\frac{1}{2}$absin∠C（∠C是a、b两边的夹角）
【问题应用】
已知平行四边形ABCD（图4）中，AB=b，BC=a，∠B=α（0°＜α＜90°）
求：平行四边形ABCD的面积．（用含a、b、α的代数式表示）

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

17．

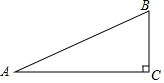如图，在△ABC中，∠C=90°，BC=5，AB=13，则sinB是（　　）

A．

$\frac{5}{13}$

B．

$\frac{5}{12}$

C．

$\frac{12}{13}$

D．

$\frac{13}{12}$

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

4．下列方程中关于x的一元二次方程的是（　　）

A．

x²+$\frac{1}{{x}^{2}}$=0

B．

x³+x-1=0

C．

x²-2xy+y²=0

D．

x²+2x-3=0

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

14．

王林同学利用暑假参观了幸福村果树种植基地（如图），他出发沿（1，3），（-3，3），（-4，0），（-4，-3），（2，-2），（5，-3），（5，0），（5，4）的路线进行了参观，请你按他参观的顺序写出他路上经过的地方，并用线段依次连接他经过的地点．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

1．春节期间，某商场计划购进甲、乙两种商品，已知购进甲商品2件和乙商品3件共需270元；购进甲商品3件和乙商品2件共需230元．
（1）求甲、乙两种商品每件的进价分别是多少元？
（2）商场决定甲商品以每件40元出售，乙商品以每件90元出售，为满足市场需求，需购进甲、乙两种商品共100件，且甲种商品的数量不少于乙种商品数量的4倍，请你求出获利最大的进货方案，并求出最大利润．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

18．下列命题中是真命题的是（　　）

	A．	经过直线外一点，有且仅有一条直线与一线与已知直线垂直
	B．	平分弦的直径垂直于弦
	C．	对角线互相平分且垂直的四边形是菱形
	D．	反比例函数y=$\frac{k}{x}$，当k＜0时，y随x的增大而增大

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

19．下列图形中，既是轴对称图形又是中心对称图形的是（　　）

A．

B．

C．

D．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学