

分析 (1)用待定系数法求出抛物线解析式,从而求出点E坐标;
(2)由对称性判断出FA=FB,再判断出△BPE∽△ACF即可;
(3)设出点M,N的坐标表示出MG,GD,DH,HN,判断出△MGD∽△DHN,再利用互余即可.
解答 解:(1)∵抛物线y=-x2+bx+3与x轴交于点A(-1,0),B(-3,0)
又a=-1,
∴y=-(x+1)(x+3),
∴y=-x2-4x-3
∵y=-x2-4x-3=-(x+2)2+1
∴E(-2,0)
(2)如图1,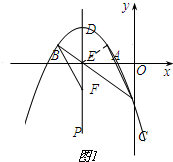
设BC与对称轴交于点F,连接AF.
∵B(-3,0),C(0,-3)
∴∠OBC=45°
∵A、B两点关于对称轴对称,
∴FA=FB,
∴∠OBC=∠FAB=45°,
∴AF⊥BC,
∵∠BPD=∠BCA,
∴△BPE∽△ACF,
∴$\frac{PE}{BE}=\frac{CF}{AF}=2$
∴PE=2,
∴P1(-2,-2),
由对称性可知,P2(-2,2),
(3)垂直.如图2,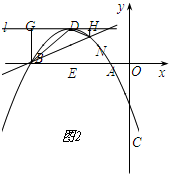
过点D作x轴的平行线l,分别过点M、N作MG⊥l,NH⊥l.
设过点E(-2,0)的直线的解析式为:y=kx+b,
则:-2k+b=0,
即:b=2k,
∴y=kx+2k,
设M(m,-m2-4m-3),N(n,-n2-4n-3),
则:MG=1+m2+4m+3=(m+2)2,GD=-2-m,
DH=n+2,HN=1+n2+4n+3=(n+2)2,
∴$\frac{MG}{GD}=\frac{(m+2)^{2}}{-2-m}$=-m-2,$\frac{DH}{NH}=\frac{n+2}{(n+2)^{2}}$=$\frac{1}{n+2}$,
∵$\left\{\begin{array}{l}{y=-{x}^{2}-4x-3}\\{y=kx+2k}\end{array}\right.$,
∴x2+(4+k)x+(3+2k)=0,
∴m+n=-4-k,mn=3+2k,
∴(m+2)(n+2)=mn+2(m+n)+4=-3+2k-8-2k+4=-1,
∴-m-2=$\frac{1}{n+2}$
∴$\frac{MG}{GD}=\frac{DH}{HN}$
∵∠G=∠H=90°
∴△MGD∽△DHN
∴∠HDN=∠GMD
∵∠GMD+∠GDM=90°
∴∠HDN+∠GDM=90°
即:DM⊥DN.
点评 此题是二次函数综合题,主要考查待定系数法求解析式,对称的性质,相似三角形性质和判定,解本题的关键是表示出线段.


科目:初中数学 来源: 题型:解答题
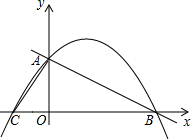 如图,在直角坐标系中,已知直线y=-$\frac{1}{2}$x+4与y轴交于A点,与x轴交于B点,C点的坐标为(-2,0).
如图,在直角坐标系中,已知直线y=-$\frac{1}{2}$x+4与y轴交于A点,与x轴交于B点,C点的坐标为(-2,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
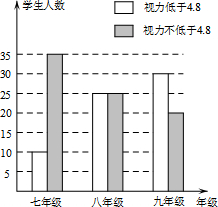 在学习了“普查与抽样调查”之后,某校八(1)班数学兴趣小组对该校学生的视力情况进行了抽样调查,并画出了如图所示的条形统计图.请根据图中信息解决下列问题:
在学习了“普查与抽样调查”之后,某校八(1)班数学兴趣小组对该校学生的视力情况进行了抽样调查,并画出了如图所示的条形统计图.请根据图中信息解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 班级 | 平均数(分) | 中位数(分) | 众数(分) |
| (1)班 | 24 | 24 | 24 |
| (2)班 | 24 | 24 | 21 |
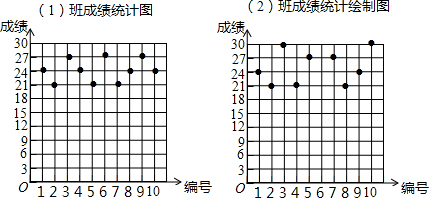
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
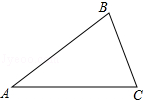 已知:在△ABC中,AB=AC.
已知:在△ABC中,AB=AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
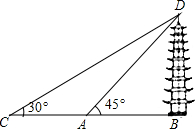 五一节,某校数学兴趣小组的同学相约去东台西溪“海春轩塔”参观,并测量其高度.如图,塔身BD与地面垂直,他们先在A处测得塔顶端点D的仰角为45°,再沿着BA的方向后退16cm至C处,测得塔顶端点D的仰角为30°,求“海春轩塔”BD的高度.($\sqrt{3}$≈1.73,结果保留一位小数)
五一节,某校数学兴趣小组的同学相约去东台西溪“海春轩塔”参观,并测量其高度.如图,塔身BD与地面垂直,他们先在A处测得塔顶端点D的仰角为45°,再沿着BA的方向后退16cm至C处,测得塔顶端点D的仰角为30°,求“海春轩塔”BD的高度.($\sqrt{3}$≈1.73,结果保留一位小数)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
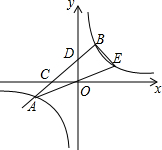 如图,直线AB与双曲线交于点A,B,与x轴,y轴分别交于点C,D,与x轴的夹角α满足tanα=$\frac{3}{4}$,且OD=6,CD:CB=1:2.
如图,直线AB与双曲线交于点A,B,与x轴,y轴分别交于点C,D,与x轴的夹角α满足tanα=$\frac{3}{4}$,且OD=6,CD:CB=1:2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com