
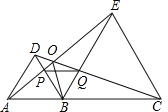
【题目】如图,已知点A、B、C在同一直线上,△ABD和△BCE都是等边三角形.则在下列结论中:①AP=DQ,②EP=EC,③PQ=PB,④∠AOB=∠BOC=∠COE.正确的结论是 (填写序号).

【答案】①③④.
【解析】
试题分析:易证△ABE≌△DBC,则有∠BAE=∠BDC,从而可证到△ABP≌△DBQ,则有AP=DQ,BP=BQ,由∠PBQ=60°可得△BPQ是等边三角形,则有PQ=PB.∠BPQ=60°,从而可得∠EPB>∠EBP,即可得到EB>EP,即EC>EP,由△ABE≌△DBC可得S△ABE=S△DBC,AE=DC,从而可得点B到AE、DC的距离相等,因而点B在∠AOC的角平分线上,即可得到∠AOB=∠BOC=∠COE=60°.
解:∵△ABD和△BCE都是等边三角形,
∴BD=BA=AD,BE=BC=EC,∠ABD=∠CBE=60°,
∵点A、B、C在同一直线上,
∴∠DBE=180°﹣60°﹣60°=60°,
∴∠ABE=∠DBC=120°.
在△ABE和△DBC中,
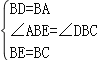 ,
,
∴△ABE≌△DBC,
∴∠BAE=∠BDC.
在△ABP和△DBQ中,
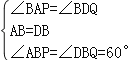 ,
,
∴△ABP≌△DBQ,
∴AP=DQ,BP=BQ.
∴①正确.
∵∠PBQ=60°,
∴△BPQ是等边三角形,
∴PQ=PB.∠BPQ=60°.
∴③正确.
∵∠EPB>∠BPQ,∠BPQ=∠EBP=60°,
∴∠EPB>∠EBP,
∴EB>EP,
∴EC>EP,
∴②不正确.
∵∠DPA=∠PDO+∠DOP,∠DPA=∠PAB+∠ABP,∠PDO=∠PAB,
∴∠DOP=∠ABP=60°,
∴∠COE=60°,∠AOC=120°.
∵△ABE≌△DBC,
∴S△ABE=S△DBC,AE=DC,
∴点B到AE、DC的距离相等,
∴点B在∠AOC的角平分线上,
∴∠AOB=∠BOC=![]() ∠AOC=60°,
∠AOC=60°,
∴∠AOB=∠BOC=∠COE=60°.
∴④正确.
故答案为①③④.


科目:初中数学 来源: 题型:
【题目】阅读理解:
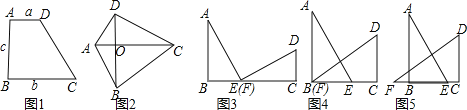
方法准备:
我们都知道:如图1,在四边形ABCD中,AD∥BC,∠B=90°,若AD=a,BC=b,AB=c,那么四边形ABCD的面积S=![]() .
.
如图2,在四边形ABCD中,两条对角线AC⊥BD,垂足为O,则四边形ABCD的面积=![]() AC×OD+
AC×OD+![]() AC×OB=
AC×OB=![]() AC×(OD+OB)=
AC×(OD+OB)=![]() AC×BD.
AC×BD.
解决问题:
(1)我们以a、b 为直角边,c为斜边作两个全等的直角△ABE与△FCD,再拼成如图3所示的图形,使B,E,F,C四点在一条直线上(此时E,F重合),可知△ABE≌△FCD,AE⊥DF. 请你证明:a2+b2=c2.
(2)固定△FCD,再将△ABE沿着BC平移到如图4所示的位置(此时B,F重合),请你继续证明:a2+b2=c2.
(3)当△ABE平移到如图5的位置,结论a2+b2=c2还成立吗?如果成立,请写出证明过程;如果不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D点在BC上,现有下列四个命题:
①若AB=AC,则∠B=∠C;
②若AB=AC,∠1=∠2,则AD⊥BC,BD=DC;
③若AB=AC,BD=CD,则AD⊥BC,∠1=∠2;
④若AB=AC,AD⊥BC,则BD=BC,∠1=∠2.
其中正确的有( )
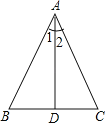
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句中,真命题有( )个
①在同一平面内,过一点有且只有一条直线与已知直线平行;
②相等的角是对顶角;
③若两个角有公共顶点且有一条公共边,和等于平角,则这两个角为邻补角;
④平方根和立方根相等的数是0;
⑤平移变换中,各组对应点连成的线段平行且相等.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,前2分钟其速度v(米/分)与时间t(分)满足二次函数v=at2,后三分钟其速度v(米/分)与时间t(分)满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分,求:

(1)二次函数和反比例函数的关系式.
(2)弹珠在轨道上行驶的最大速度.
(3)求弹珠离开轨道时的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件中,不能判定△ABC是等腰三角形的是( )
A.a=3,b=3,c=4 B.a︰b︰c=2︰3︰4
C.∠B=50°,∠C=80° D.∠A︰∠B︰∠C=1︰1︰2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com