
����Ŀ����ѧϰ�˵����¡�������ƽ��ͼ�Ρ���֪ʶ��С�����Լ����е�һ�����ǰ������ֱ�Ƕ��������һ��ƴ�����µ�ͼ��1��ͼ��2��
��1����ͼ1�У���ADƽ����BACʱ��С����Ϊ��ʱABҲӦ��ƽ����FAD������ͨ�������ж�С���Ľ����Ƿ���ȷ��
��2��С�������֣�ֻҪAD����BAC���ڲ�������ABC��ֱ�Ƕ���A��תʱ��������FAB=��DAC����ͼ2���������ж�С���ķ����Ƿ���ȷ�����������ɣ�
��3����ͼ2�У�����FAC=x����BAD=y������̽��x��y�Ĺ�ϵ��

���𰸡�(1)�����������2��С���Ľ�����ȷ�����������������3��y=180�㩁x��90��x��180�㣩��
��������
��1������ADƽ����BAC�������BAD=45��������FAD=90���������FAB=45��������֤��ABƽ����FAD.��2��������BAD+��CAD=90�㣬��FAB+��BAD=90�㣬����֤����FAB=��DAC����3��������FAB=��FAC��90��=90��-��BAD���ɵó���.
��1��С���Ľ�����ȷ���������£�
��ADƽ����BAC����BAD+��CAD=90�㣬
���BAD=��CAD=45�㣮
�ߡ�FAB+��BAD=90�㣬
���FAB=45�㣬
���FAB=��BAD��
��ABƽ����FAD��
��2��С���Ľ�����ȷ���������£�
�ߡ�BAD+��CAD=90�㣬��FAB+��BAD=90�㣬
���FAB=��DAC��
��3���ߡ�FAC=��FAB+90�㣬
���FAB=��FAC��90�㣮
�ߡ�BAD=90�㩁��FAB��
���BAD=180�㩁��FAC����y=180�㩁x��90��x��180�㣩��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ϱ�����һЩ�ص�ķֲ�ʾ��ͼ����ͼ�У��ֱ�����������������Ϊ![]() �ᡢ
�ᡢ![]() �����������ƽ��ֱ������ϵ���������ĸ����ۣ�
�����������ƽ��ֱ������ϵ���������ĸ����ۣ�
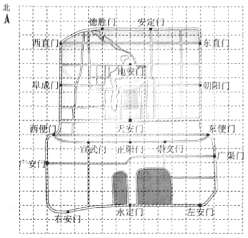
�ٵ���ʾ�찲�ŵĵ������Ϊ��0��0������ʾ�㰲�ŵĵ������Ϊ��![]() ��
��![]() ��ʱ����ʾ���ŵĵ������Ϊ��5��
��ʱ����ʾ���ŵĵ������Ϊ��5��![]() ����
����
�ڵ���ʾ�찲�ŵĵ������Ϊ��0��0������ʾ�㰲�ŵĵ������Ϊ��![]() ��
��![]() ��ʱ����ʾ���ŵĵ������Ϊ��10��
��ʱ����ʾ���ŵĵ������Ϊ��10��![]() ����
����
�۵���ʾ�찲�ŵĵ������Ϊ��1��1������ʾ�㰲�ŵĵ������Ϊ��![]() ��
��![]() ��ʱ����ʾ���ŵĵ������Ϊ��
��ʱ����ʾ���ŵĵ������Ϊ��![]() ��
��![]() ����
����
�ܵ���ʾ�찲�ŵĵ������Ϊ��![]() ��
��![]() ������ʾ�㰲�ŵĵ������Ϊ��
������ʾ�㰲�ŵĵ������Ϊ��![]() ��
��![]() ��ʱ����ʾ���ŵĵ������Ϊ��
��ʱ����ʾ���ŵĵ������Ϊ��![]() ��
��![]() ����
����
���������У�������ȷ���۵������
A. �٢ڢ� B. �ڢۢ� C. �٢� D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֽ���й����е��������.����ͼ��ʾ���ĸ���ֽͼ����.������Գ�ͼ���������ĶԳ�ͼ�ε��ǣ� ��
A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���õ����������Σ���������ABCD�߳�Ϊa��С������CEFG�߳�Ϊb��a��b����M��BC����һ�����㣬����AM��MF��MF��CG�ڵ�P������ABM�Ƶ�A��ת����ADN������MEF�Ƶ�F��תǡ������NGF�����������������ۣ��١�AND=��MPC�� �ڡ�ABM�ա�NGF����S�ı���AMFN=a2+b2��
������ȷ�Ľ�����_____������д��ţ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵȱ���BCD�У�DF��BC�ڵ�F����AΪֱ��DF��һ���㣬��BΪ��ת���ģ���BA˳ʱ�뷽����ת60����BE������EC��
(1)����A���߶�DF���ӳ�����ʱ��
����֤��DA=CE��
���ж���DEC����EDC��������ϵ����˵�����ɣ�
(2)����DEC=45��ʱ������AC������BAC�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�İ뾶OD����AB�ڵ�C������AO���ӳ�����O�ڵ�E������EC.��AB=8��CD=2����EC�ij���
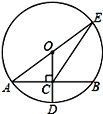
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪D��BC���е㣬����D��BC�Ĵ��߽���BAC��ƽ�����ڵ�E��EF��AB�ڵ�F��EG��AC�ڵ�G��
��1����֤��BF��CG��
��2����AB��10��AC��6�����߶�CG�ij�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�D��AC��һ��(CD��AD)����Ҫ��������и�С�⣮(������ͼ�ۼ�����д������������������ĸ)
(1)����BD��������DEF(��E���߶�CD�ϣ���F���߶�AC���Ҳ�)��ʹ����DEF�ա�DAB��
(2)��(1)�������£�����EFH����ABC����CA���ӳ����ڵ�H����֤��HF��BC.

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com