
【题目】如图,点P是菱形ABCD对角线AC上的一点,连接DP并延长DP交边AB于点E,连接BP并延长交边AD于点F,交CD的延长线于点G. 
(1)求证:△APB≌△APD;
(2)已知DF:FA=1:2,设线段DP的长为x,线段PF的长为y. ①求y与x的函数关系式;
②当x=6时,求线段FG的长.
【答案】
(1)证明:∵点P是菱形ABCD对角线AC上的一点,
∴∠DAP=∠PAB,AD=AB,
∵在△APB和△APD中
 ,
,
∴△APB≌△APD(SAS)
(2)解:①∵△APB≌△APD,
∴DP=PB,∠ADP=∠ABP,
∵在△DFP和△BEP中,
 ,
,
∴△DFP≌△BEP(ASA),
∴PF=PE,DF=BE,
∵四边形ABCD是菱形,
∴GD∥AB,
∴ ![]() =
= ![]() ,
,
∵DF:FA=1:2,
∴ ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∵ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴y= ![]() x;
x;
②当x=6时,y= ![]() ×6=4,
×6=4,
∴PF=PE=4,DP=PB=6,
∵ ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得:FG=5,
故线段FG的长为5
【解析】(1)根据菱形的性质得出∠DAP=∠PAB,AD=AB,再利用全等三角形的判定得出△APB≌△APD;(2)①首先证明△DFP≌△BEP,进而得出 ![]() =
= ![]() ,
, ![]() =
= ![]() ,进而得出
,进而得出 ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,即可得出答案; ②根据①中所求得出PF=PE=4,DP=PB=6,进而得出
,即可得出答案; ②根据①中所求得出PF=PE=4,DP=PB=6,进而得出 ![]() =
= ![]() =
= ![]() ,求出即可.
,求出即可.
【考点精析】关于本题考查的菱形的性质和相似三角形的判定与性质,需要了解菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能得出正确答案.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】已知:关于x的二次函数y=﹣x2+ax(a>0),点A(n,y1)、B(n+1,y2)、C(n+2,y3)都在这个二次函数的图象上,其中n为正整数.
(1)y1=y2 , 请说明a必为奇数;
(2)设a=11,求使y1≤y2≤y3成立的所有n的值;
(3)对于给定的正实数a,是否存在n,使△ABC是以AC为底边的等腰三角形?如果存在,求n的值(用含a的代数式表示);如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,顶点A、C分别在x,y轴的正半轴上.点Q在对角线OB上,且QO=OC,连接CQ并延长CQ交边AB于点P.则点P的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.Rt△ABC内接于⊙O,BC为直径,AB=4,AC=3,D是 ![]() 的中点,CD与AB的交点为E,则
的中点,CD与AB的交点为E,则 ![]() 等于( )
等于( ) 
A.4
B.3.5
C.3
D.2.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在不透明的袋子中有四张标着数字1,2,3,4的卡片,小明、小华两人按照各自的规则玩抽卡片游戏. 小明画出树状图如图所示:
小华列出表格如下:
第一次 | 1 | 2 | 3 | 4 |
1 | (1,1) | (2,1) | (3,1) | (4,1) |
2 | (1,2) | (2,2) | ① | (4,2) |
3 | (1,3) | (2,3) | (3,3) | (4,3) |
4 | (1,4) | (2,4) | (3,4) | (4,4) |
回答下列问题:
(1)根据小明画出的树形图分析,他的游戏规则是,随机抽出一张卡片后(填“放回”或“不放回”),再随机抽出一张卡片;
(2)根据小华的游戏规则,表格中①表示的有序数对为;
(3)规定两次抽到的数字之和为奇数的获胜,你认为谁获胜的可能性大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于两个相似三角形,如果沿周界按对应点顺序环绕的方向相同,那么称这两个三角形互为顺相似;如果沿周界按对应点顺序环绕的方向相反,那么称这两个三角形互为逆相似.例如,如图①,△ABC∽△A′B′C′,且沿周界ABCA与A′B′C′A′环绕的方向相同,因此△ACB和△A′B′C′互为顺相似;如图②,△ABC∽△A′B′C′,且沿周界ABCA与A′B′C′A′环绕的方向相反,因此△ACB和△A′B′C′互为逆相似.
(1)根据图Ⅰ,图Ⅱ和图Ⅲ满足的条件.可得下列三对相似三角形:①△ADE与△ABC;②△GHO与△KFO;③△NQP与△NMQ;其中,互为顺相似的是;互为逆相似的是 . (填写所有符合要求的序号).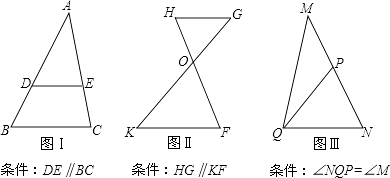

(2)如图③,在锐角△ABC中,∠A<∠B<∠C,点P在△ABC的边上(不与点A,B,C重合).过点P画直线截△ABC,使截得的一个三角形与△ABC互为逆相似.请根据点P的不同位置,探索过点P的截线的情形,画出图形并说明截线满足的条件,不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系xOy中,O为坐标原点,点P是反比例函数y= ![]() (x>0)图象上的一个动点,若以点P为圆心,3为半径的圆与直线y=x相交,交点为A,B,当弦AB的长等于2
(x>0)图象上的一个动点,若以点P为圆心,3为半径的圆与直线y=x相交,交点为A,B,当弦AB的长等于2 ![]() 时,点P的坐标为( )
时,点P的坐标为( ) 
A.(1,6)和(6,1)
B.(2,3)和(3,2)??
C.( ![]() ,3
,3 ![]() )和(3
)和(3 ![]() ,
, ![]() )
)
D.( ![]() ,2
,2 ![]() )和(2
)和(2 ![]() ,
, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com