
【题目】二次函数y1=ax2+2x过点A(﹣2,0)和点B,过点A,B作一次函数y2=kx+b,若点B的横坐标为1.
(1)求出二次函数与一次函数的解析式;
(2)根据图象,当y2>y1时,请直接写出x的取值范围;
(3)若P点在抛物线y1上,且横坐标为﹣1,求△ABP的面积.

【答案】(1)y2=x+2;(2)当﹣2<x<1时,y2>y1;(3)3.
【解析】
(1)利用待定系数法求二次函数与一次函数的解析式;
(2)根据图象直接写出y2>y1时,-2<x<1;
(3)过P作PQ∥y轴,交AB于Q,依据S△ABP=S△APQ+S△BPQ进行计算即可.
解:(1)如图1,
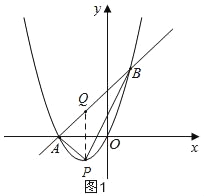
把A(﹣2,0)代入y1═ax2+2x中得:
4a+2×(﹣2)=0,
a=1,
∴二次函数的解析式y1═x2+2x,
当x=1时,y1=1+2=3,
∴B(1,3),
把A(﹣2,0)、B(1,3)代入y2=kx+b中得:
![]() ,
,
解得:![]() ,
,
∴一次函数的解析式:y2=x+2;
(2)由图象得:当﹣2<x<1时,y2>y1;
(3)过P作PQ∥y轴,交AB于Q,
y1═x2+2x,令x=﹣1,则y=﹣1,即P(﹣1,﹣1),
y2=x+2,令x=﹣1,则y=1,即Q(﹣1,1),
∴PQ=2,
∴S△ABP=S△APQ+S△BPQ=![]() ×2×(1+2)=3.
×2×(1+2)=3.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
【题目】已知A(n,-2),B(1,4)是一次函数y=kx+b的图象和反比例函数y=![]() 的图象的两个交点,直线AB与y轴交于点C.
的图象的两个交点,直线AB与y轴交于点C.
(1)求反比例函数和一次函数的关系式;
(2)求△AOC的面积;
(3)求不等式kx+b-![]() <0的解集(直接写出答案).
<0的解集(直接写出答案).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮玩一种游戏:三张大小,质地都相同的卡片上分别标有数字1,2,3,现将标有数字的一面朝下,小明从中任意抽取一张,记下数字后放回洗匀,然后小亮从中任意抽取一张,计算小明和小亮抽得的两个数字之和,如果和为奇数,则小明胜,若和为偶数则小亮胜.
(1)用列表或画树状图等方法,列出小明和小亮抽得的数字之和所有可能出现的情况.
(2)请判断该游戏对双方是否公平?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子里装着质地、大小都相同的 3 个红球和 2 个绿球,随机从中摸出一球,不再放回袋中,充分搅匀后再随机摸出一球,两次都摸到红球的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+2x+a2,当x=m时,函数值y<0,则当x=m+2时,函 数值y( )
A. 小于 B. 等于0 C. 大于0 D. 与0的大小不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置高为1.5米的测角仪AB,在A处测得电线杆上C处的仰角为30°,求拉线CE的长(结果保留小数点后一位,参考数据:![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为美化环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米.
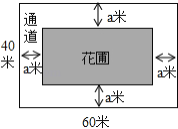
(1)当a=10米时,花圃的面积=
(2)通道的面积与花圃的面积之比能否恰好等于3:5,如果可以,求出此时通道的宽.
查看答案和解析>>
科目:初中数学 来源: 题型:
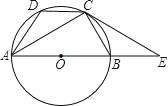
【题目】如图,AB是⊙O的直径,点C、D在⊙O上,且AC平分∠BAD,点E为AB的延长线上一点,且∠ECB=∠CAD.
(1)①填空:∠ACB= ,理由是 ;
②求证:CE与⊙O相切;
(2)若AB=6,CE=4,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交与BE的延长线于点F,且AF=DC,连结CF.

(1)求证:四边形ADCF是平行四边形;
(2)当AB与AC有何数量关系时,四边形ADCF为矩形,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com