
 ��ƽ��ֱ������ϵxOy�У�������y=mx2-2mx-3��m��0����x�ύ��A��B���㣬�ҵ�A������Ϊ��3��0����
��ƽ��ֱ������ϵxOy�У�������y=mx2-2mx-3��m��0����x�ύ��A��B���㣬�ҵ�A������Ϊ��3��0�������� ��1������Գ��ᣬ���ݶԳ��������B���꣬���ô���ϵ�������m��ֵ��
��2������ͼ������ͼ�ɽ�����⣮
��3����ֱ��y=kx+1�����㣨$\frac{1}{2}$��-$\frac{15}{4}$��ʱ��k=-$\frac{19}{2}$���Ƴ�ֱ��y=kx+1��k��0����ͼ��M��ֱ��$x=\frac{1}{2}$���IJ���ֻ��һ�������㣬��ͼ���֪k��-$\frac{19}{2}$����ֱ��y=kx+1�����㣨-1��0��ʱ��k=1����ʱֱ��y=kx+1Ҳ�����������ɴ˼��ɽ�����⣮
��� �⣺��1���������ߵĶԳ���x=1����A���꣨3��0����
�֡�A��B���ڶԳ���Գƣ�
��B��-1��0����
�ѵ�B��-1��0������õ�0=m+2m-3��
��m=1��
��2����ͼ����ͼ���֪����-2��x��3ʱ��-4��y��5��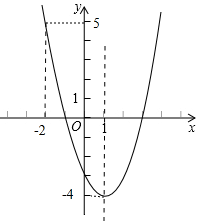
��3������������x���Ϸ��IJ�����x�ᷭ�ۣ������ߵ����ಿ�ֱ��ֲ��䣬�õ�һ����ͼ��M����ͼ��ʾ��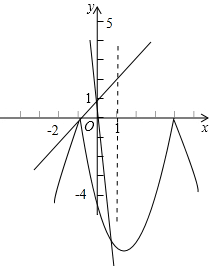
��x=$\frac{1}{2}$ʱ��y=$\frac{1}{4}$-1-3=-$\frac{15}{4}$��
�൱ֱ��y=kx+1�����㣨$\frac{1}{2}$��-$\frac{15}{4}$��ʱ��k=-$\frac{19}{2}$��
��ֱ��y=kx+1��k��0����ͼ��M��ֱ��$x=\frac{1}{2}$���IJ���ֻ��һ�������㣬��ͼ���֪k��-$\frac{19}{2}$��
��ֱ��y=kx+1�����㣨-1��0��ʱ��k=1����ʱֱ��y=kx+1Ҳ����������
����������k��ȡֵ��ΧΪk��-$\frac{19}{2}$��k=1��
���� ���⿼����������x��Ľ��㡢һ�κ���������ϵ������֪ʶ������Ĺؼ���ѧ����ȷ��������ͼ������ͼ������⣬�����п��������ͣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2cm��13cm��13cm | B�� | 4cm��4cm��4cm | C�� | 3cm��4cm��7cm | D�� | 1cm��$\sqrt{2}$ cm��$\sqrt{3}$ cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 1����3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪������y=-$\frac{1}{2}$x2+x+4��y�ύ��C����x�ύ�ڵ�A��B��ƽ����x��Ķ�ֱ��l�������߽��ڵ�P��ֱ��AC���ڵ�F����D������Ϊ��2��0�����ʣ��Ƿ����������ֱ��l��ʹ�á�ODF�ǵ��������Σ������ڣ���ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
��֪������y=-$\frac{1}{2}$x2+x+4��y�ύ��C����x�ύ�ڵ�A��B��ƽ����x��Ķ�ֱ��l�������߽��ڵ�P��ֱ��AC���ڵ�F����D������Ϊ��2��0�����ʣ��Ƿ����������ֱ��l��ʹ�á�ODF�ǵ��������Σ������ڣ���ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
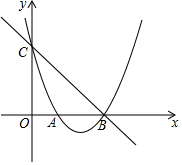 ��ͼ��������y=$\frac{1}{2}$x2-3x+4��ͼ����x�ύ��A��B���㣬��y�ύ�ڵ�C����P��ֱ��BC���˶������߶�AP����СֵΪ$\sqrt{2}$��
��ͼ��������y=$\frac{1}{2}$x2-3x+4��ͼ����x�ύ��A��B���㣬��y�ύ�ڵ�C����P��ֱ��BC���˶������߶�AP����СֵΪ$\sqrt{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
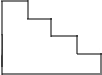 ��̨�ײ���ʾ��ͼ�У�̨��1�ף�ˮƽ����2.5�ף�Ϊӭ�ӹ����Ҫ��̨�����̿���2�ĵ�̺����Ŀ�����˾������������г��Ϲ���ÿƽ����200Ԫ��̺����Ҫ�������ֽ�
��̨�ײ���ʾ��ͼ�У�̨��1�ף�ˮƽ����2.5�ף�Ϊӭ�ӹ����Ҫ��̨�����̿���2�ĵ�̺����Ŀ�����˾������������г��Ϲ���ÿƽ����200Ԫ��̺����Ҫ�������ֽ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��2 | B�� | 2 | C�� | -2 | D�� | m��-2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3Ԫ | B�� | 4Ԫ | C�� | 5Ԫ | D�� | 8Ԫ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com