
如图,已知⊙O为Rt△ABC的内切圆,切点为D、E、F,半径为r,∠C=90°,AB、BC、AC的长分别为c、a、b,求证: .
.

|
连结OD、OE、OF,则OD⊥BC,OE⊥AB,OF⊥AC.
∴四边形CDOF为正方形,CF=CD=DO=OF=r. 由O是内心,得∠1=∠2. 在Rt△AOF和Rt△AOE中, ∵∠1=∠2,∠AFO=∠AEO=90°,AF=AE, ∴Rt△AOF≌Rt△AOE. ∴AF=AE. 同理可证BD=BE. ∵AF=AC-CF=b-r,BD=BC-CD=a-r, ∴AE+BE=AF+BD=b-r+a-r=AB=c. ∴2r=a+b-c,即  . . |
|
求证的结论是内切圆的半径为r与Rt△ABC的三边之间的关系,因此必须将r代换到△ABC的边上去.显然四边形CDOE是正方形,则CD=CF=r. 由AF=b-r,BD=a-r,不难看出AF=AE,BD=BE,因而b-r+a-r=c,问题得证.
|


科目:初中数学 来源: 题型:
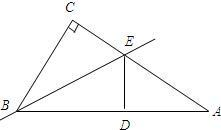 如图,已知,在Rt△ABC中,∠C=90°,沿过B点的一条直线BE折叠这个三角形,使C点与AB边上的一点D重合.
如图,已知,在Rt△ABC中,∠C=90°,沿过B点的一条直线BE折叠这个三角形,使C点与AB边上的一点D重合.查看答案和解析>>
科目:初中数学 来源: 题型:
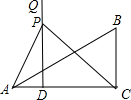 重合),过D作DQ⊥AC(DQ与AB在AC的同侧);点P从D点出发,在射线DQ上运动,连接PA、PC.
重合),过D作DQ⊥AC(DQ与AB在AC的同侧);点P从D点出发,在射线DQ上运动,连接PA、PC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com