
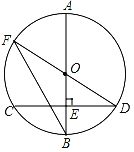
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,点F在⊙O上,FD恰好经过圆心O,连接FB.
(1)若∠F=∠D,求∠F的度数;
(2)若CD=24,BE=8,求⊙O的半径.
【答案】(1)30°;(2)13.
【解析】试题分析:
(1)由OB=OF可得∠F=∠B,结合∠BOD=∠B+∠F可得∠BOD=2∠F,结合∠F=∠D,可得∠BOD=2∠D,由CD⊥AB可得∠D+∠BOD=90°,由此可得3∠D=90°,∠D=30°;
(2)由AB是⊙O的直径,CD=24,弦CD⊥AB可得DE=12,设⊙O的半径为![]() ,则OD=
,则OD= ![]() ,OE=
,OE= ![]() ,在Rt△ODE中由勾股定理建立方程即可解出
,在Rt△ODE中由勾股定理建立方程即可解出![]() .
.
试题解析:
(1)∵OF=OB,
∴∠B=∠F,
∴∠DOB=∠B+∠F=2∠B,
∵∠DOE+∠D=90°
∴2∠B+∠D=90°,
∵∠B=∠D,
∴2∠D+∠D=90°,
∴∠D=30°;
(2)设⊙O的半径为r,
∵AB⊥CD,
∴CE=DE=![]() CD=
CD=![]() ×24=12,
×24=12,
在Rt△ODE中,OE=OB-BE=r-8,OD=r,
∵OE2+DE2=OD2,
∴(r-8)2+122=r2,解得r=13,
∴⊙O的半径为13.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将坐标原点O沿x轴向左平移2个单位长度得到点A,过点A作y轴的平行线交反比例函数![]() 的图象于点B,AB=
的图象于点B,AB=![]() .
.
(1)求反比例函数的解析式;
(2)若P(![]() ,
, ![]() )、Q(
)、Q(![]() ,
, ![]() )是该反比例函数图象上的两点,且
)是该反比例函数图象上的两点,且![]() 时,
时, ![]() ,指出点P、Q各位于哪个象限?并简要说明理由.
,指出点P、Q各位于哪个象限?并简要说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
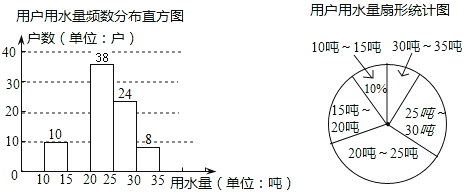
【题目】某市为提倡节约用水,准备实行自来水阶梯计算方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为了更好地决策,自来水公司随机抽取了部分用户的用水量数据,并绘制了如图不完整的统计图,(每组数据包括在右端点但不包括左端点),请你根据统计图解答下列问题:
(1)此次抽样调查的样本容量是___________
(2)补全频数分布直方图,求扇形图中“15吨~20吨”部分的圆心角的度数.
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区10万用户中约有多少用户的用水全部享受基本价格?
查看答案和解析>>
科目:初中数学 来源: 题型:
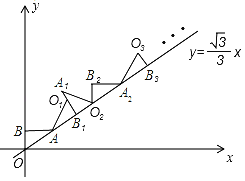
【题目】如图,点B的坐标是(0,1),AB⊥y轴,垂足为B,点A在直线y=![]() x,将△ABO绕点A顺时针旋转到△AB1O1的位置,使点B的对应点B1落在直线y=
x,将△ABO绕点A顺时针旋转到△AB1O1的位置,使点B的对应点B1落在直线y=![]() x上,再将△AB1O1绕点B1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=
x上,再将△AB1O1绕点B1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=![]() x上,依次进行下去…,则点O100的纵坐标是_____.
x上,依次进行下去…,则点O100的纵坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为1的正方形网格图中,点B的坐标为(2,0),点A的坐标为(0,-3).
(1)在图1中,请建立合适的坐标系,把线段AB绕原点旋转180°得线段DE(其中A与D是对应点),则四边形ABDE是 形,面积等于 .
(2)在图2中,仅使用无刻度的直尺,作出以AB为边的矩形ABFG,使其面积为11(保留作图痕迹,不写做法)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)解方程组或不等式组
①解方程组
②解不等式组 把解集在数轴上表示出来,并写出不等式组的负整数解.
把解集在数轴上表示出来,并写出不等式组的负整数解.
(2)甲、乙两位同学一起解方程组 ,由于甲看错了方程①中的
,由于甲看错了方程①中的![]() ,得到的解为
,得到的解为![]() ,乙看错了方程②中的
,乙看错了方程②中的![]() ,得到的解为
,得到的解为![]() ,试计算的
,试计算的![]() 值.
值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师对试卷讲评课中九年级学生参与的深度与广度进行评价调查,每位学生最终评价结果为主动质疑、独立思考、专注听讲、讲解题目四项中的一项.评价组随机抽取了若干名初中学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:


(1)在这次评价中,一共抽查了名学生;
(2)在扇形统计图中,项目“主动质疑”所在扇形的圆心角度数为度;
(3)请将频数分布直方图补充完整;
(4)如果全市九年级学生有8000名,那么在试卷评讲课中,“独立思考”的九年级学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣2x+m﹣1=0有两个实数根.
(1)求m的取值范围;
(2)设p是方程的一个实数根,且满足(p2﹣2p+3)(m+4)=7,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果将(a+b)n(n为非负整数)的每一项按字母a的次数由大到小排列,可以得到下面的等式(1),然后将每个式子的各项系数排列成(2):(a+b)1=a+b;(a+b)2=a2+2ab+b2;(a+b)3=a3+3a2b+3ab2+b3;(a+b)4=a4+4a3b+6a2b2+4ab3+b4;根据规律可得:(a+b)5=_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com