
���� ��1�������ܷ��õ����������Դ��ۺ�ĵ��ۣ���y��=640��0.85x����������������ܷ��ã��������ۣ���0��x��20ʱ��y��=640��0.9x����x��20ʱ��y��=640��0.9��20+640��0.75��x-20����
��2���������ۣ���0��x��20����Ȼy����y������x��20������y��=544x��y��=480x+1920������y����y���Ĵ�С�в���ʽ���ɵã�
��� �⣺��1������������ܷ��ã�y��=640��0.85x=544x��
����������ܷ��ã�
��0��x��20ʱ��y��=640��0.9x=576x��
��x��20ʱ��y��=640��0.9��20+640��0.75��x-20��=480x+1920��
��2����0��x��20��y��=544x��y��=576x��
����y����y������ѡ��������磻
��x��20������y��=544x��y��=480x+1920��
�ٵ�y����y������544x��480x+1920����ã�x��30��
�ʵ�20��x��30ʱ��ѡ��������磻
�ڵ�y��=y������544x=480x+1920����ã�x=30��
�ʵ�x=30ʱ������������һ����
�۵�y����y������544x��480x+1920����ã�x��30��
�ʵ�x��30ʱ��ѡ���������磮
���ϣ����μ����ε���������30��ʱ��ѡ��������磻���μ����е���������30��ʱ�����Ҷ�һ�������μ����е���������30��ʱ��ѡ���������磮
���� ���⿼����һ�κ�����Ӧ�ã�����ʵ�������е�������ϵ����һ�κ�����ϵ���ر������������ܷ���Ҫ���÷ֶκ���������⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ������� | ���ۼ۸� |
| ������30�� | ����40Ԫ |
| ����30�� | ÿ����1������������г������۽���0.5Ԫ�������۲��õ���30Ԫ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
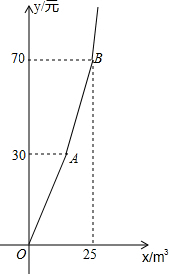 Ϊ��ǿ��·�Ľ�ˮ��ʶ����������ˮ��Դ��ij�жԾ�����ˮʵ�н���ˮ�ۣ������ͥÿ����ˮ������Ϊ�������ݣ�һ����������ˮ�ĵ���֮�ȵ���1��2����ͼ���߱�ʾʵ�н���ˮ�ۺ�ÿ��ˮ��y��Ԫ������ˮ��x��m3��֮��ĺ�����ϵ����������AB��ʾ�ڶ�������ʱy��x֮��ĺ�����ϵ��
Ϊ��ǿ��·�Ľ�ˮ��ʶ����������ˮ��Դ��ij�жԾ�����ˮʵ�н���ˮ�ۣ������ͥÿ����ˮ������Ϊ�������ݣ�һ����������ˮ�ĵ���֮�ȵ���1��2����ͼ���߱�ʾʵ�н���ˮ�ۺ�ÿ��ˮ��y��Ԫ������ˮ��x��m3��֮��ĺ�����ϵ����������AB��ʾ�ڶ�������ʱy��x֮��ĺ�����ϵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com