
分析 (1)先根据所给的式子找出第一、第二、第三个式子的规律,进而可求出a10的表达式;
(2)根据所给的式子找出第一、第二、第三个式子的规律,进而可求出an的表达式;
(3)把所给式子相加,找出规律即可进行计算;
(4)根据所给规律探索可得出$\frac{1}{2×4}$=$\frac{1}{2}$×($\frac{1}{2}-\frac{1}{4}$),$\frac{1}{4×6}$=$\frac{1}{2}×(\frac{1}{4}-\frac{1}{6})$…,易得结果.
解答 解:(1)∵第1个等式:a1=$\frac{1}{1×2}$=1-$\frac{1}{2}$
第2个等式:a2=$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$
第3个等式:a3=$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$
…
∴第10个等式a10=$\frac{1}{10×11}$=$\frac{1}{10}-\frac{1}{11}$;
故答案为:$\frac{1}{10×11}$,$\frac{1}{10}-\frac{1}{11}$;
(2))∵第1个等式:a1=$\frac{1}{1×2}$=1-$\frac{1}{2}$
第2个等式:a2=$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$
第3个等式:a3=$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$
…
∴第n个等式an=$\frac{1}{n×(n+1)}$=$\frac{1}{n}-\frac{1}{n+1}$;
故答案为:$\frac{1}{n×(n+1)}$,$\frac{1}{n}-\frac{1}{n+1}$;
(3)$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…$+\frac{1}{2015×2016}$
=1-$\frac{1}{2}$+$\frac{1}{2}-\frac{1}{3}$$+\frac{1}{3}-\frac{1}{4}$+…$\frac{1}{2015}$$-\frac{1}{2016}$
=1$-\frac{1}{2016}$
=$\frac{2015}{2016}$;
(4)$\frac{1}{2×4}$+$\frac{1}{4×6}$+$\frac{1}{6×8}$+…+$\frac{1}{1000×1002}$
=$\frac{1}{2}$×($\frac{1}{2}-\frac{1}{4}$)+$\frac{1}{2}$×($\frac{1}{4}-\frac{1}{6}$)+$\frac{1}{2}×(\frac{1}{6}-\frac{1}{8})$+…+$\frac{1}{2}$×$(\frac{1}{1000}-\frac{1}{1002})$
=$\frac{1}{2}$×($\frac{1}{2}-\frac{1}{1002}$)
=$\frac{125}{501}$.
点评 题考查的是有理数的混合运算,是一道找规律的题目,关键是通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题,熟练掌握分数的拆分计算.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
 如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,从左起第1个等边三角形的边长记为a1,第2个等边三角形的边长记为a2,以此类推.若OA1=1,则a2016=22015.
如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,从左起第1个等边三角形的边长记为a1,第2个等边三角形的边长记为a2,以此类推.若OA1=1,则a2016=22015.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
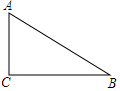 如图,在△ABC中,∠C=90°,AC=3,BC=4,以点A为圆心,4为半径作⊙A,则( )
如图,在△ABC中,∠C=90°,AC=3,BC=4,以点A为圆心,4为半径作⊙A,则( )| A. | 点B在⊙A外 | B. | 点B在⊙A上 | ||
| C. | 点B在⊙A外内 | D. | 点B与⊙A的位置关系不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com