

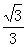 x+5 (2)t=5
x+5 (2)t=5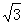 ;t=
;t=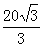
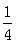 t2;10<t≤20时,S=-
t2;10<t≤20时,S=-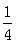 t2+5t
t2+5t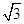 .那么A(0,5),C(5
.那么A(0,5),C(5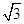 ,0),设直线AC的解析式为y=ax+b,代入A,C两点,得y=-
,0),设直线AC的解析式为y=ax+b,代入A,C两点,得y=-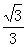 x+5
x+5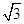 s
s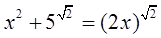 ,即X=
,即X=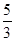
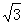 ,加上前面的5
,加上前面的5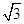 ,得到t=
,得到t=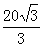
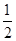 tx
tx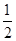 =
=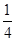
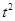
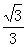 m+5),再由5-(
m+5),再由5-(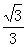 m+5)=(t-10)x
m+5)=(t-10)x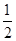 得出Q点的纵坐标为10-
得出Q点的纵坐标为10-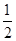 t,围成的三角形面积=tx(10-
t,围成的三角形面积=tx(10-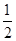 t )x
t )x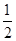 =-
=-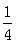 t2+5t
t2+5t

 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的图象如图所示.
的图象如图所示.
 ,求二次函数的解析式;
,求二次函数的解析式; ,点
,点 是x轴上的一个动点.若在(1)的条件下,过点P垂直于x轴的直线交这个一次函数的图象于点M,交二次函数
是x轴上的一个动点.若在(1)的条件下,过点P垂直于x轴的直线交这个一次函数的图象于点M,交二次函数 的图象于点N.若只有当1<m<
的图象于点N.若只有当1<m< 时,点M位于点N的上方,求这个一次函数的解析式;
时,点M位于点N的上方,求这个一次函数的解析式; 有实数根,请你构造恰当的函数,根据图象直接写出
有实数根,请你构造恰当的函数,根据图象直接写出 的最大值.
的最大值.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 米,某天小敏从家里出发骑自行车上学,开始她以每分钟
米,某天小敏从家里出发骑自行车上学,开始她以每分钟 米的速度匀速行驶了
米的速度匀速行驶了 米,遇到交通堵塞,耽搁了
米,遇到交通堵塞,耽搁了 分钟,然后以每分钟
分钟,然后以每分钟 米的速度匀速前进一直到学校
米的速度匀速前进一直到学校 ,你认为小敏离家的距离
,你认为小敏离家的距离 与时间
与时间 之间的函数图象大致是( )
之间的函数图象大致是( )
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 :y=3x+1与直线
:y=3x+1与直线 :y=mx+n相交于点P(1,b).
:y=mx+n相交于点P(1,b).
 ,请你直接写出它的解;
,请你直接写出它的解; :y=nx+m是否也经过点P?请说明理由.
:y=nx+m是否也经过点P?请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com