

���� ��1�����˽���ٵ���30�ˣ�ռ50%������ý����ʾ������ѧ�������̶��������ͳ��ͼ�С������˽⡱��������Ӧ���ε�Բ�Ľǣ�
��2���ɣ�1��������˽���������̶���ȫ����ͳ��ͼ��
��3������������������ķ�����������ô𰸣�
��� �⣺��1�����˽���ٵ���30�ˣ�ռ50%��
������ʾ������ѧ�����У�30��50%=60���ˣ���
������ͳ��ͼ�С������˽⡱��������Ӧ���ε�Բ�Ľ�Ϊ��$\frac{15}{60}$��360��=90�㣻
�ʴ�Ϊ��60��90��
��2��60-15-30-10=5��
��ȫ����ͳ��ͼ�ã�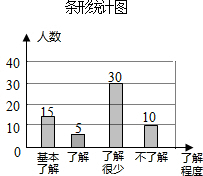
��3����������ã�900��$\frac{15+5}{60}$=300���ˣ���
����Ƹ���ѧѧ���ж�У��ȫ֪ʶ�ﵽ���˽⡱�͡������˽⡱�̶ȵ�������Ϊ300�ˣ�
���� ���⿼�����б�������״ͼ��������Լ�����ͳ��ͼ������ͳ��ͼ���ؼ��Ǹ����б�������״ͼ��������Լ�����ͳ��ͼ������ͳ��ͼ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017��ɽ��ʡ���������������꼶ѧҵˮƽ���Ե�һ��ģ����ѧ�Ծ��������棩 ���ͣ���ѡ��
����ͼ���У�������Գ�ͼ���������ĶԳ�ͼ�ε���( )
A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
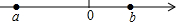 ��ͼ��a��b�������ϵ����㣬����$\sqrt{{a^2}-2ab+{b^2}}$+$\sqrt{{a^2}+2ab+{b^2}}$=-2a��
��ͼ��a��b�������ϵ����㣬����$\sqrt{{a^2}-2ab+{b^2}}$+$\sqrt{{a^2}+2ab+{b^2}}$=-2a���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -4û�������� | B�� | 1���������ǡ�1 | C�� | $\frac{1}{36}$����������$\frac{1}{6}$ | D�� | -5����������-$\root{3}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
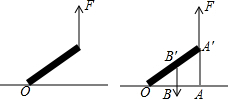 ��ͼ�����������߸��������������F�ķ���ʼ����ֱ���ϣ�����߸�����������������Ĵ�С����������
��ͼ�����������߸��������������F�ķ���ʼ����ֱ���ϣ�����߸�����������������Ĵ�С����������| A�� | ��� | B�� | ��С | C�� | ���� | D�� | ���ж� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ֪����ʽ��$\left\{\begin{array}{l}x+2a��1\\ 2x-b��3\end{array}$�Ľ⼯��ͼ��ʾ����a-b��ֵΪ0��
֪����ʽ��$\left\{\begin{array}{l}x+2a��1\\ 2x-b��3\end{array}$�Ľ⼯��ͼ��ʾ����a-b��ֵΪ0���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
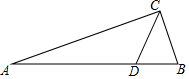 ��ͼ��ʾ����Rt��ABC�У�б��AB=3��BC=1����D��AB�ϣ���$\frac{BD}{AD}$=$\frac{1}{3}$����tan��BCD��ֵ�ǣ�������
��ͼ��ʾ����Rt��ABC�У�б��AB=3��BC=1����D��AB�ϣ���$\frac{BD}{AD}$=$\frac{1}{3}$����tan��BCD��ֵ�ǣ�������| A�� | $\frac{1}{3}$ | B�� | 1 | C�� | $\frac{2\sqrt{2}}{3}$ | D�� | $\frac{3\sqrt{3}}{2}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com